Chapter 1: Introduction to the Multiplication Trick

Multiplication can be represented visually by creating diagonal lines and counting their intersections. This method can be quite fascinating and insightful.

The illustration above demonstrates how to execute the multiplication of 32 and 24. The pink lines symbolize the number 32 (three lines for the tens place and two for the units), while the blue lines represent 24 (two lines for the tens and four for the units). To find the product, we begin by counting the points where the lines intersect.

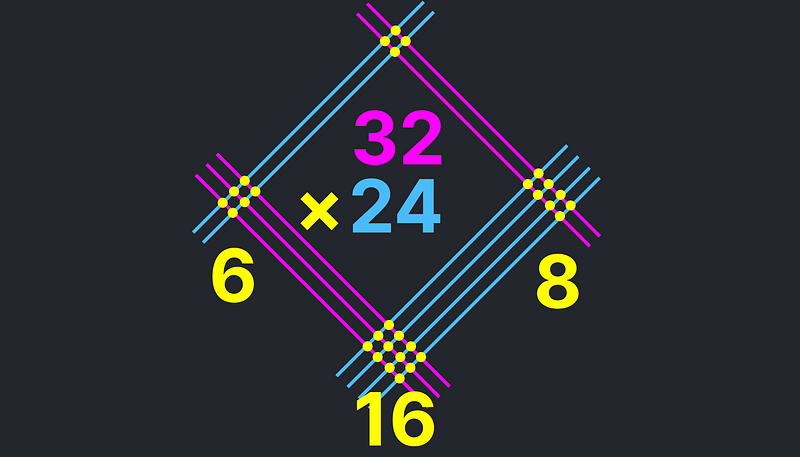
In our counting, we identify 6 from the left column, 16 from the middle column, and 8 from the right column. By adding these values according to their place values (remembering to carry the 1 from 16), we compute:

32 × 24 = 768

or equivalently,

32 × 24 = 600 + 160 + 8 = 768.

One interesting aspect of this technique is that it allows for rotation of the diagram to find products with the same digits. For instance, rotating it 90° counterclockwise yields the product of 24 and 32.

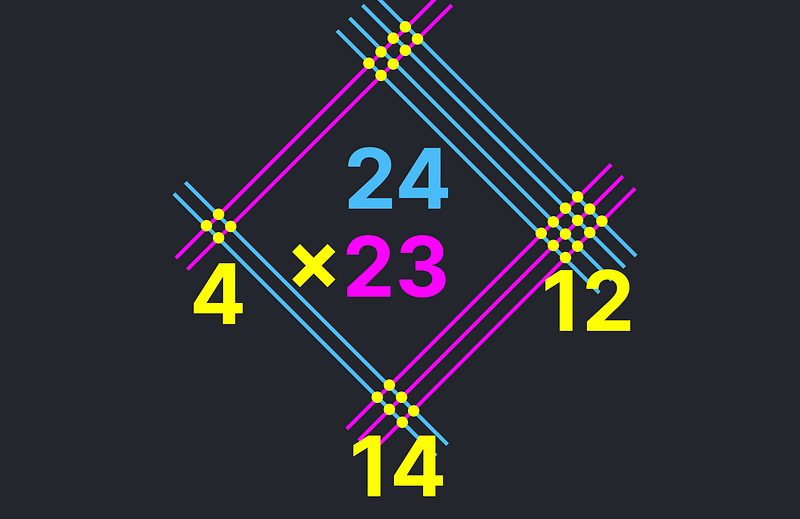
By adding in columns again, we find:

400 + 140 + 12 = 552.

Can you grasp how the trick operates? By concentrating on a single set of intersection points first, it becomes clear that 3 parallel lines intersecting with 4 parallel lines yield 3 × 4 = 12 points. This exemplifies the essence of multiplication — it is, in fact, repeated addition.

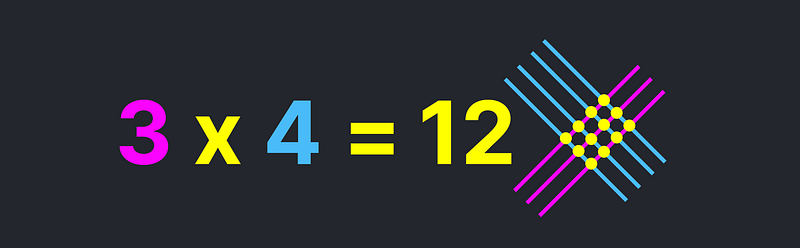
The subsequent steps in the algorithm mirror the conventional column multiplication method. Observing the leftmost column, where each line signifies 10, we find that the intersection points correspond to 20 × 20 = 400.

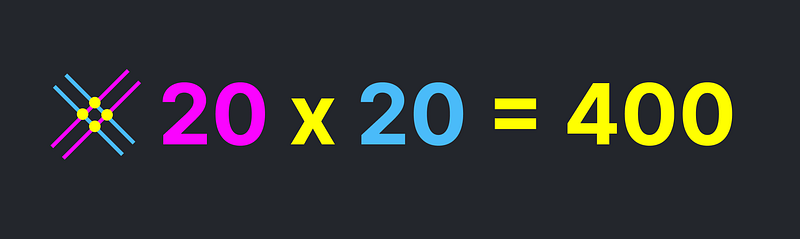
The middle column serves as a “tens column,” as one line from each set represents tens, while the other represents units.

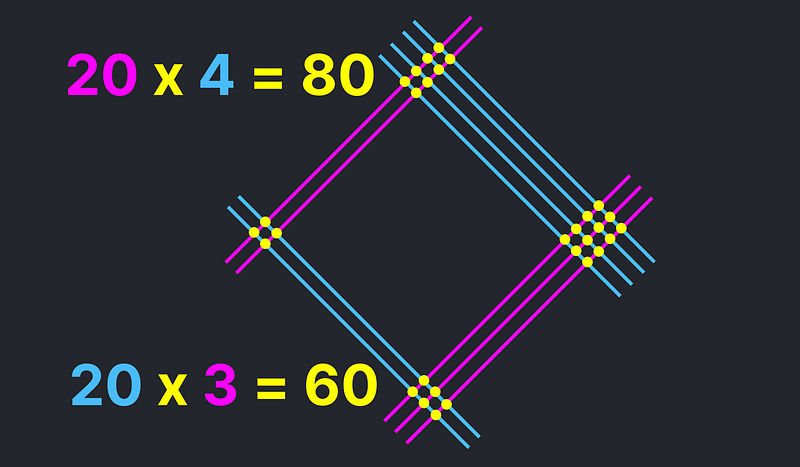
It's crucial to align the columns accurately. Utilizing two perpendicular sets of lines can assist in this task. Here's an example involving three-digit numbers:

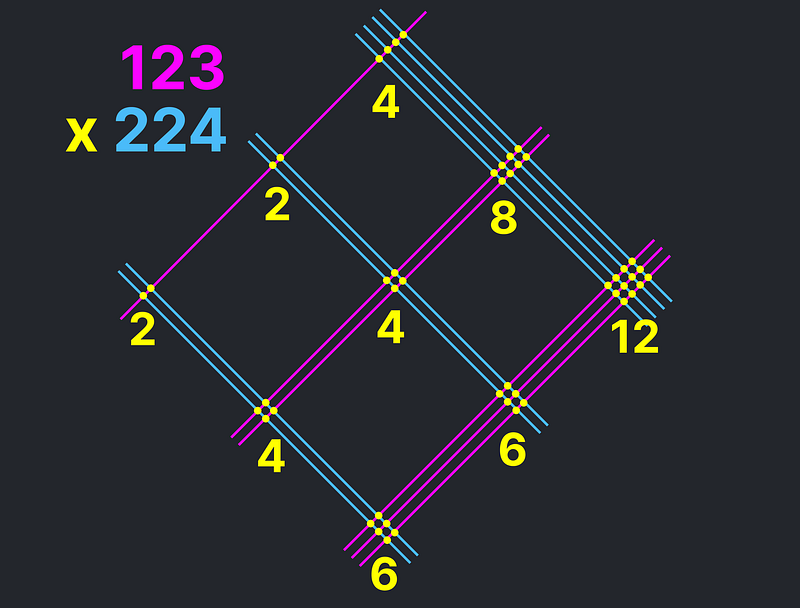
From the diagram above, we can determine that:

122 × 224 = 20000 + (2000 + 4000) + (400 + 400 + 600) + (80 + 60) + 12 = 27552.

This method is quite intriguing! However, is it practical? Perhaps not entirely. The traditional method of stacking numbers and processing from right to left is generally more efficient (not just because of familiarity). Counting intersection points when we already know that 3 × 4 = 12 can feel a bit tedious.

Consider the task of using this line method for calculating 9 × 9 = 81!

Nonetheless, exploring alternative methods and understanding their foundations is a valuable part of the rich tapestry that is mathematics.

Chapter 2: Practical Applications and Video Resources

To further explore multiplication techniques, check out these informative videos:

The first video titled "Multiplication Trick | Full-Time Kid | PBS Parents" provides engaging insights into multiplication tricks that can make learning fun.

The second video, "Cool math mental multiplication trick - become a genius solving math instantly!" showcases exciting mental multiplication strategies.