# Exploring Deep Boltzmann Machines and Their Cosmic Implications
Written on
Chapter 1: Understanding Deep Boltzmann Machines
If our universe is indeed a computation in progress, it is plausible that evidence of such computation can be found within the universe's structure. Generative Adversarial Networks (GANs) represent a machine learning technique that enabled a computer program to defeat the world's top GO player—a game so intricate that many believed a machine could never surpass human skill. This article seeks to present circumstantial evidence suggesting that the principles behind GANs are inherently embedded in the fabric of our universe.
Section 1.1: An Introduction to Generative Adversarial Networks
GANs are a class of models that employ deep learning techniques for generative tasks. Among the various deep learning methods, Restricted Boltzmann Machines (RBMs) and GANs stand out. A Deep Boltzmann Machine (DBM) consists of multiple stacked RBMs, characterized by undirected connections between layers. GANs were created to address the limitations of traditional deep learning frameworks like DBMs.
The following graph illustrates a Boltzmann Machine, showcasing hidden (h) and visible (v) nodes.
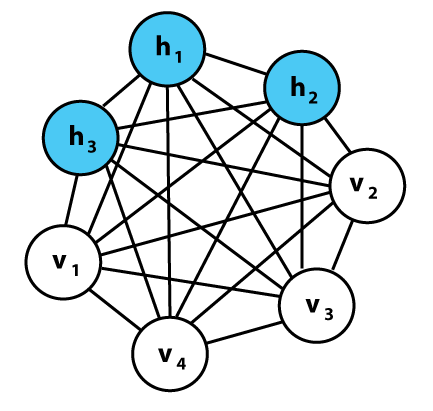
Section 1.2: The Nature of Boltzmann Machines
In a Boltzmann Machine, there is no distinct separation between the input and output layers. Visible nodes receive inputs, and these nodes also return reconstructed outputs. This is facilitated through bidirectional weights that allow information to flow in both directions, ensuring that every node is interconnected. All connections are bidirectional, and the weights are symmetrical.
Generative modeling is an unsupervised machine learning task that identifies patterns in input data, enabling the computer to create new examples that closely resemble those in the original dataset. The GAN framework comprises two models: the generator, which creates new examples, and the discriminator, which evaluates whether these examples are authentic or fabricated.
The generator and discriminator undergo simultaneous training. The generator produces a set of samples, which, together with real data, are assessed by the discriminator. In subsequent iterations, the discriminator is refined to better distinguish between real and fake examples, while the generator adjusts based on its effectiveness in deceiving the discriminator. As Dr. Jason Brownlee explains:
> The generator can be likened to a counterfeiter attempting to produce fake currency, while the discriminator functions as law enforcement, striving to identify genuine currency and catch counterfeit notes. For the counterfeiter to prevail, they must create currency indistinguishable from the authentic version.
Chapter 2: AdS/CFT and the Deep Boltzmann Machine
According to Koji Hashimoto, Deep Boltzmann Machines represent a specialized type of neural network utilized in deep learning for modeling the probabilistic distributions of datasets. The AdS/CFT correspondence describes a holographic duality between a (d+1)-dimensional quantum gravity framework and a d-dimensional quantum field theory (QFT) that lacks gravity. The latter resides at the boundary of the former's gravitational spacetime, referred to as bulk spacetime.
Hashimoto posits that the conventional AdS/CFT correspondence can be interpreted as a Deep Boltzmann Machine. When appropriately defined, the neural network architecture resembles bulk spacetime geometry. From the QFT perspective, the direction perpendicular to the boundary surface represents an “emergent” spatial dimension. The structure of Deep Boltzmann Machines aligns with the AdS/CFT framework, provided we equate their visible layers with the QFT and their hidden layers with the bulk spacetime.
In summary, Hashimoto indicates that the hidden nodes of a Deep Boltzmann Machine correspond to the bulk spacetime within an Anti-de Sitter (AdS) black hole, while the visible nodes are represented on the boundary of that black hole. This line of reasoning suggests that our universe manifests as a projection on a boundary within a black hole. Moreover, it is proposed that the computation conducted by our universe resembles a less constrained variant of a Deep Boltzmann Machine, specifically a GAN.
Section 2.1: The Role of Forgetting in Deep Learning
According to Carlos Perez, deep learning networks excel at retaining information but struggle with forgetting. The ability to forget is vital for developing enduring abstractions. Advanced deep learning systems utilize attention mechanisms to simplify the input space and focus on critical components, effectively allowing them to ignore what remains constant.
Forgetting, or the act of discarding memory, is a process that involves consolidating experiences into a generalized form. Activation functions serve as threshold mechanisms that influence the flow of information both during inference and back-propagation, representing a basic method for managing memory changes within deep learning networks.
Recent studies on biological brains suggest that learning new tasks does not necessarily involve forgetting, but rather the reuse of existing neurons. The mechanism of forgetting is believed to occur during the consolidation of existing modules. Both evolution and the brain do not continually invent new components; instead, they rewire what is already present. In the context of evolution, this concept is referred to as pre-adaptation.
By reconfiguring existing structures, we do not forget; we repurpose. This approach, while not always optimal, aligns with the principle of least action, which suggests that the most natural actions are those that require minimal effort. Our free will can serve as a tool for repurposing, with our emotional responses to past and present experiences shaping how we choose to reorganize information.
Section 2.2: The Principle of Least Action
The principle of least action in physics aligns with the notion that the fundamental aim of reality is to enhance complexity. As discussed in earlier articles, the mathematical concept of entropy can help establish guidelines for increasing complexity. Identifying methods to boost complexity also entails minimizing the action necessary to achieve that complexity, in accordance with a principle that seeks to reduce any increase in entropy.
The next discussion will delve into Constructor Theory (CT), which arises from the necessity of bulk spacetime to continually advance in complexity. CT comprises principles that dictate the laws of physics, fostering increases in complexity, with the principle of least action being one of these foundational tenets. Consequently, the actions of forgetting or repurposing align with the pursuit of greater complexity.
The central question posed in this article is:
Can you embrace creativity through the act of forgetting?