Harnessing Mathematical Thinking for Data Analysis and Prediction
Written on
Chapter 1: Introduction to Mathematical Thinking
Mathematical thinking serves as a cornerstone in the realm of computer science, playing a crucial role in everything from creating efficient algorithms to optimizing data structures. This piece delves into the importance of mathematical thinking, showcasing its relevance in problem-solving, algorithm formulation, and the foundational theories underlying computing.
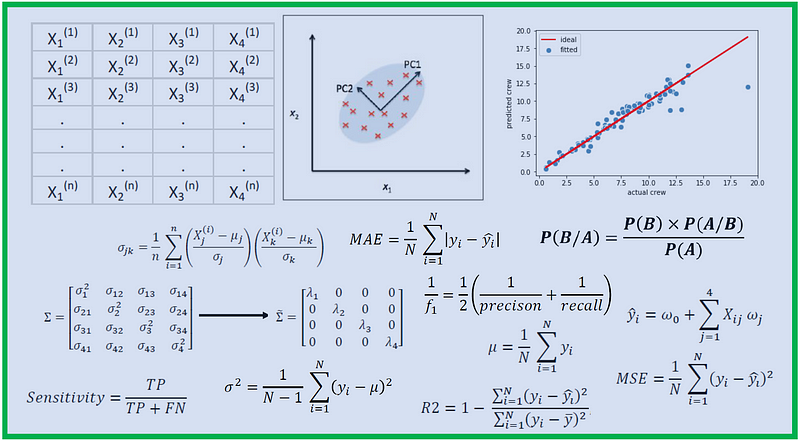
In the expansive field of computer science, mathematical thinking acts as a guiding compass, enabling professionals to navigate complex datasets and unveil valuable insights.
The Essence of Mathematical Thinking
Mathematical thinking transcends mere numbers and equations; it embodies a problem-solving approach that prioritizes clarity, precision, and logical reasoning. This method involves deconstructing intricate problems into simpler components, recognizing patterns, formulating hypotheses, and rigorously testing solutions. In computer science, this analytical mindset is essential for crafting algorithms, optimizing processes, and ensuring the reliability and efficacy of software systems.
Problem-Solving and Algorithms
At the core of computer science lies the creation of algorithms—systematic procedures for addressing challenges. Mathematical thinking is vital for algorithm development, enabling computer scientists to envision abstract processes and translate them into actionable steps. Through mathematical evaluation, algorithms can be fine-tuned for optimal performance, measured by time and space complexity, which are critical factors in computing efficiency.
Data Structures and Optimization
Mathematical thinking is also fundamental in designing and enhancing data structures—methods for organizing and storing data to facilitate efficient access and modification. By employing mathematical concepts such as graphs, trees, and matrices, computer scientists can engineer data structures that significantly improve software application performance, resulting in faster and more resource-efficient systems.
Theoretical Foundations and Innovation
The theoretical aspects of computer science, including computational complexity, automata theory, and cryptography, are deeply rooted in mathematical thinking. These domains leverage mathematical principles and techniques to probe the boundaries of computation, assess algorithmic efficiency, and safeguard data. Moreover, mathematical thinking drives innovation in emerging fields like machine learning, quantum computing, and artificial intelligence, where sophisticated mathematical models and algorithms are crucial for progress.
Case Studies and Applications
Practical examples of mathematical thinking's application in computer science are abundant. For instance, mathematical algorithms are utilized in network design to optimize routing and enhance communication robustness. In the realm of machine learning, statistical models and optimization algorithms underpin the development of systems capable of learning from data and evolving over time. These applications illustrate the transformative impact of mathematical thinking on technology and society.
Using Mathematics and Computational Thinking - YouTube
This video explores how mathematical principles and computational thinking can be applied to solve complex problems in computer science.
Mathematical Thinking in Computer Science - YouTube
This video delves into the significance of mathematical thinking in computer science, highlighting its role in algorithm design and data analysis.
Code Example: Predicting Future Values
To exemplify mathematical thinking in computer science, let's create a Python script that embodies this methodology. We will tackle a problem involving the generation of synthetic data, applying an algorithm, and utilizing mathematical concepts for analysis. Here's the structured approach:
- Problem Statement: Predict future values in a time series dataset using linear regression, a mathematical model.
- Approach:
- Generate a synthetic dataset with an identifiable pattern.
- Split the dataset into training and testing sets.
- Apply linear regression to establish the relationship.
- Evaluate the model using metrics like Mean Squared Error (MSE) and R-squared (R2).
- Analysis: Interpret the model's coefficients and performance metrics.
- Visualization: Display the results through plots.
Here’s the code:
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
import matplotlib.pyplot as plt
# 1. Generate a Synthetic Dataset
np.random.seed(0)
x = np.arange(100)
y = 0.5 * x + np.random.normal(size=x.size) * 10
# Convert to a DataFrame
data = pd.DataFrame({'X': x, 'Y': y})
# 2. Apply Linear Regression
X = data[['X']] # Features
Y = data['Y'] # Target
# Split the data into training and testing sets
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# Initialize and train the model
model = LinearRegression()
model.fit(X_train, Y_train)
# Predictions
Y_pred = model.predict(X_test)
# 3. Evaluate the Model
mse = mean_squared_error(Y_test, Y_pred)
r2 = r2_score(Y_test, Y_pred)
# Results and Interpretations
print(f'Mean Squared Error: {mse}')
print(f'R-squared: {r2}')
# 4. Plot the results
plt.scatter(X_test, Y_test, color='black', label='Actual Data')
plt.plot(X_test, Y_pred, color='blue', linewidth=3, label='Linear Regression Line')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Linear Regression on Synthetic Data')
plt.legend()
plt.show()
Interpretation
- Mean Squared Error (MSE): Represents the average squared differences between predicted and actual values.
- R-squared (R²): Indicates the proportion of variance in the dependent variable that can be explained by the independent variable(s).
The results will be visualized in a plot, showcasing the relationship between the actual data points and the linear regression line.
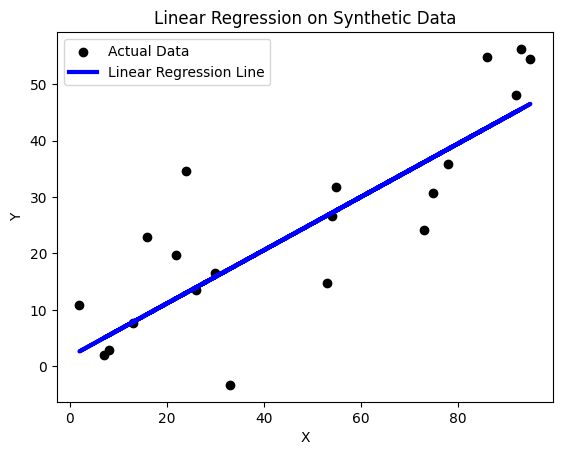
The plot illustrates the linear regression analysis on the synthetic dataset, where the scatter points represent actual data and the blue line denotes the regression model.
Conclusion
Mathematical thinking is not merely theoretical in the field of computer science; it is a vital skill that fosters innovation, efficiency, and effective problem-solving. Its influence extends across the discipline, shaping the technologies that are pivotal to contemporary life. As computer science evolves, the significance of mathematical thinking will undoubtedly remain a foundational element supporting ongoing advancements.