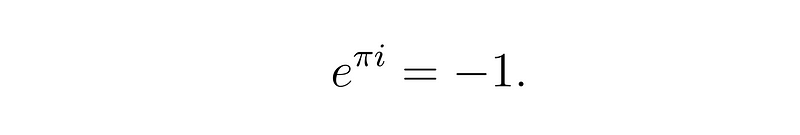Chapter 1: The Unexpected Beauty of Linear Algebra

During my time at university, one of the foundational courses I had to take was linear algebra, focusing on matrices and vector spaces. Initially, I found it rather dull and uninviting. However, I soon realized how mistaken I was about its significance.

As I delved deeper, I discovered that linear algebra serves as a fundamental tool across various branches of mathematics. Its applications range from probability theory to differential equations, group theory, and analytic number theory. It's remarkable how central matrices are to numerous mathematical disciplines, particularly graph theory, which consists of nodes and edges.

We have long studied graphs by transforming them into matrices, preserving their topological characteristics, and utilizing the comprehensive theories of linear algebra, such as eigenvalue and subspace theories, to extract insights about these graphs.

Interestingly, this relationship is reciprocal. We can also express matrices as graphs, gaining a clearer understanding of matrices through their graphical representations. For instance, the following matrix:

can be visualized as a graph:

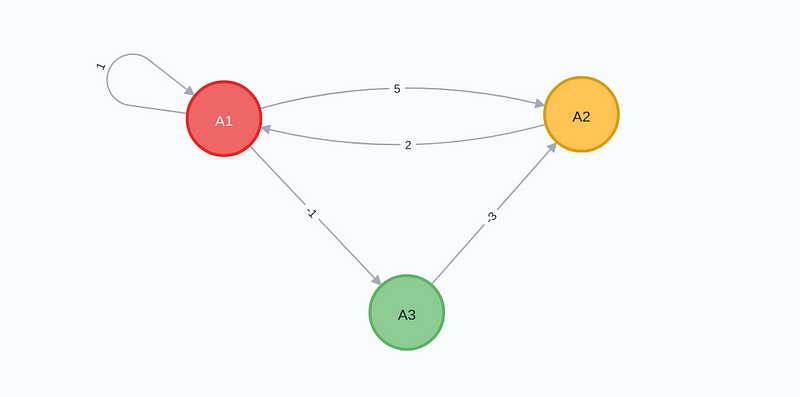
In this graph, the three nodes symbolize the three rows and columns of the matrix, while the directed and weighted edges represent the matrix's entries. For example, an edge with a weight of 5 between nodes A1 and A2 reflects the presence of the number 5 in the matrix's first row and second column. This pattern continues, with outgoing edges representing rows and incoming edges representing columns. Consequently, we can also depict vectors as graphs.

As we will soon see, this duality allows us to perform fascinating operations on graphs, such as applying functions, determining their "eigen graphs," multiplying graphs, and even calculating determinants. Moreover, we can visualize real and complex numbers using graphs, which we will explore later in this article.

Chapter 2: Graph Arithmetic and Its Revelations

A significant realization is that multiplying matrices corresponds to traversing specific paths within a graph!

Some readers may remember the formula for multiplying two matrices, particularly for 2×2 matrices, which can appear quite daunting:

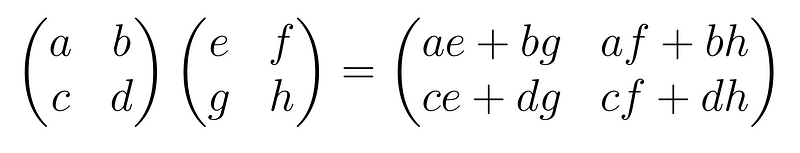
Let’s analyze this from a graphical standpoint, starting with the two graphs representing the matrices we aim to multiply:

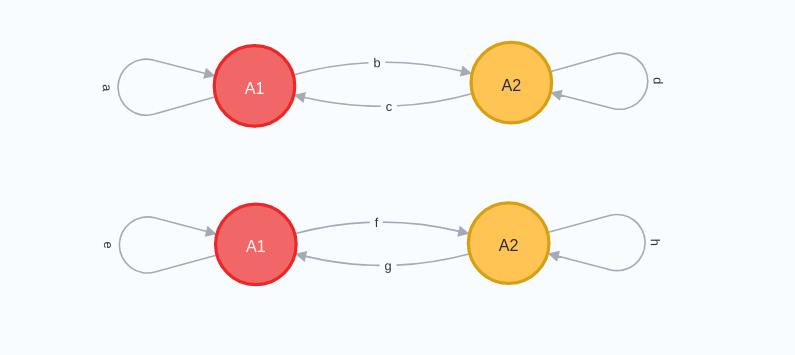
Note that the red and yellow nodes represent the same nodes; however, I intentionally separated them into two distinct graphs for clarity. We will refer to these as the "top graph" and "bottom graph."

To find the value of the first row and first column entry of the resulting matrix, we begin at node A1 and examine the paths that lead back to A1 using two "jumps"—one from the top graph (left matrix) and one from the bottom graph (right matrix).

For instance, we could traverse path a on the top graph and then follow edge e on the bottom graph, returning to A1. Alternatively, we could take path b first and then g. These paths yield the value of the top-left entry as ae + bg.

Let’s calculate another entry, specifically the bottom-left entry. To do this, we identify paths from A2 to A1 starting from the top graph. We can either take path c from A2 to A1 and then follow e back to A1, or take path d and then g. Thus, the entry becomes ce + dg.

Readers interested in further exploration can attempt to calculate the remaining entries themselves. The key takeaway is that we now possess a method to visualize both matrices and their multiplication.

Next, we will define how to multiply two graphs through graph multiplication. This will lead us to a better understanding of complex numbers.

Video: Tom Needham: Geometry and Topology of Spaces of Structured Matrices

In this video, Tom Needham discusses the intricate relationship between geometry, topology, and the structured matrices that underpin linear algebra.

Video: Matrix Multiplication as Composition | Chapter 4, Essence of Linear Algebra

This chapter from the Essence of Linear Algebra series provides a comprehensive look at how matrix multiplication can be interpreted through graphical representations.

Chapter 3: Visualizing Complex Numbers with Graphs

It’s worth noting that both real and complex numbers can be represented through matrices. For instance, a real number 'a' can be expressed as:

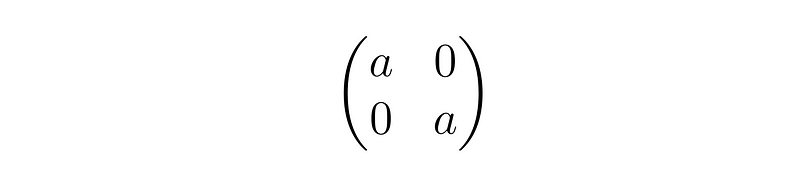
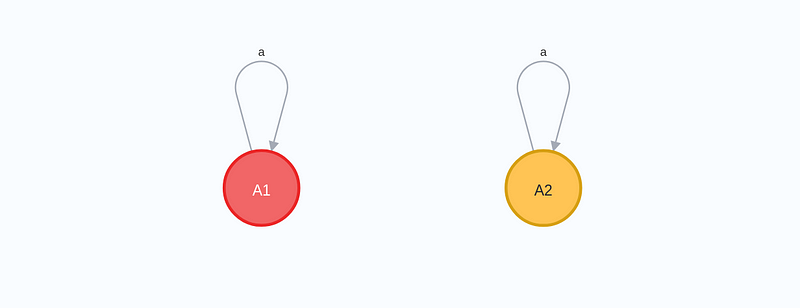
In this case, the multiplication of real numbers corresponds to matrix multiplication, while addition aligns with matrix addition. The graph representing the real number 'a' is:

Next, let’s examine how the imaginary unit 'i' can be represented:

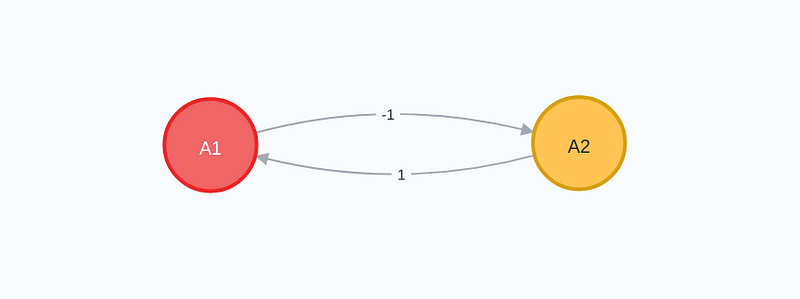
To square 'i' using graph multiplication, we only need to trace paths within a single graph. Specifically, there exists a path from A1 to itself through -1 and then 1. Hence, the resulting weight from A1 to itself is -1. There are no paths from A1 to A2 using exactly two jumps, nor from A2 to A1 under the same condition. The only path from A2 to itself involves going through 1 and then -1, resulting in -1 again. Consequently, we arrive at the following graph:

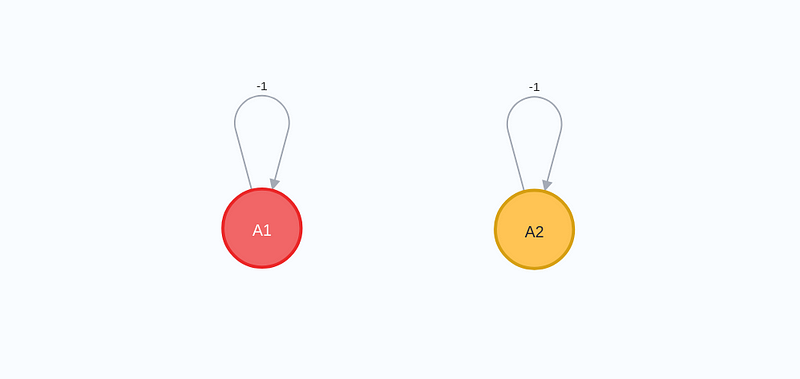
This graph accurately represents the real number -1, as expected since (i^2 = -1).

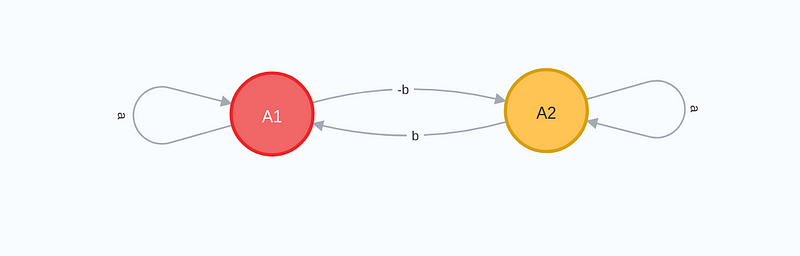
A complex number of the form (a + bi) can be visualized by combining the graphs representing (a) and (bi):

Chapter 4: Functions Applied to Graphs

Let’s define an analytic function through its power series, assuming it converges, and determine what that function accomplishes when applied to a graph. Since a power series maintains the graph structure, this process is well-defined.

For instance, consider the graph:

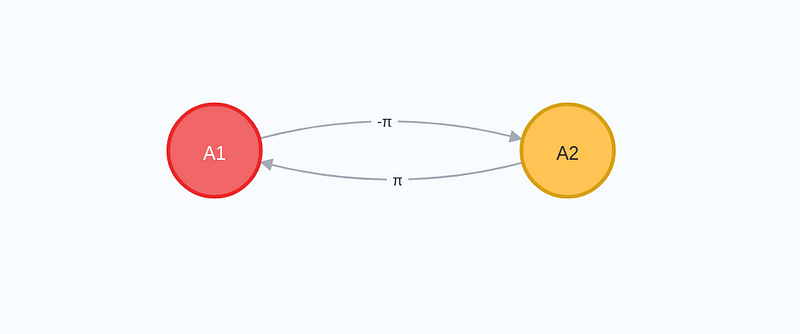
Applying the exponential function (e^x) to this graph yields a converging graph that appears as:

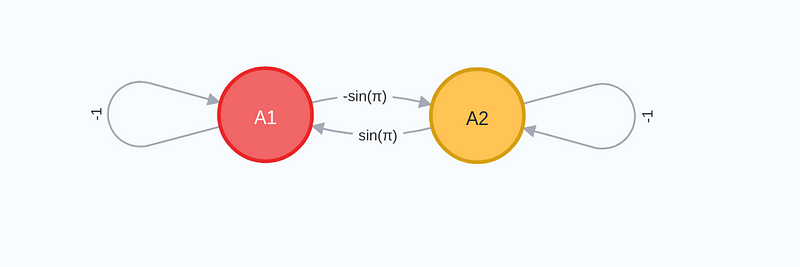
In the limit, since (sin(theta) = 0) and paths of weight zero equate to non-existent paths, the outcome of applying the exponential function to the graph is effectively:

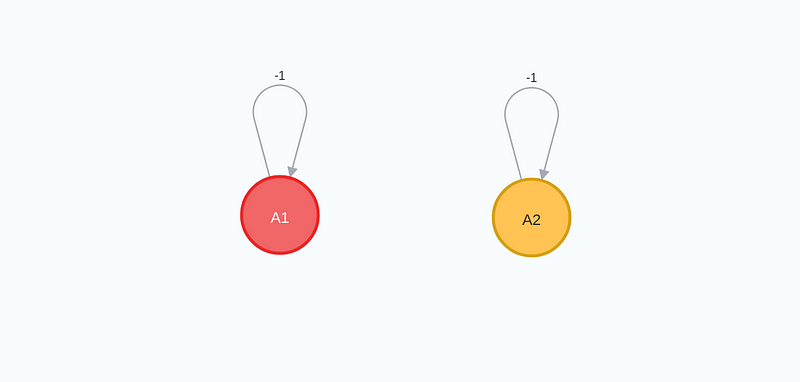
This leads us to one of the most celebrated equations in mathematics: