Mastering Calculus: The n-th Derivative of Products Simplified
Written on
Understanding the n-th Derivative of Products
The n-th derivative of a product can be surprisingly similar to a binomial expansion. We all remember from high school the method for finding the derivative of a product involving two functions, u(x) and v(x):
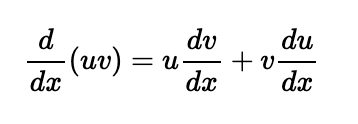
In this article, I will present an expression for the n-th derivative of a product, which bears a striking resemblance to the binomial expansion. Recall that the binomial expansion of an n-th power is expressed as follows:
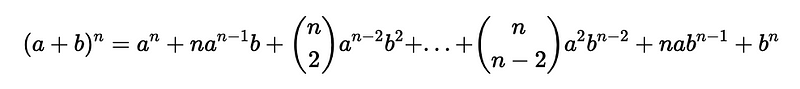
This can also be represented in another form:
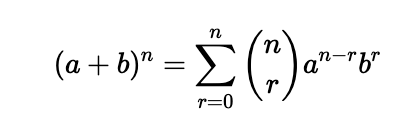
where
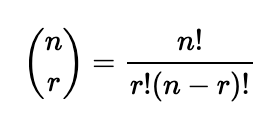
The formula for the n-th derivative of a product is:
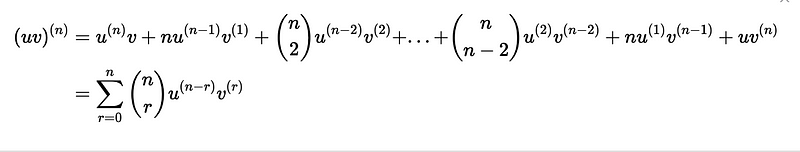
In this expression, the index (k) refers to the k-th derivative, and the zero-th derivative denotes the function itself.
Proof Using Induction
To demonstrate this result, I will employ an inductive argument. For those familiar with my writings, I often liken induction to a line of dominos that knock each other over in succession. To ensure all dominos fall, we need to confirm that the first one will fall (the base case) and that each fallen domino causes the next to fall (the inductive step).
To prove our assertion, we start with verifying it for n=1 (the base case). Then we assume it holds for n=k and use this assumption to establish that it must also hold for n=k+1 (the inductive step).
For n=1:
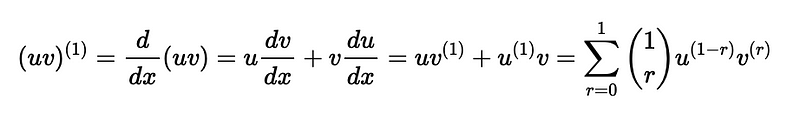
Thus, the base case is validated since it aligns with the product rule for the first derivative.
Moving on to the inductive step, we assume it holds for n=k:
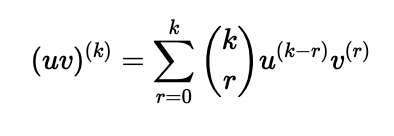
Now, we apply the product rule to differentiate this expression:
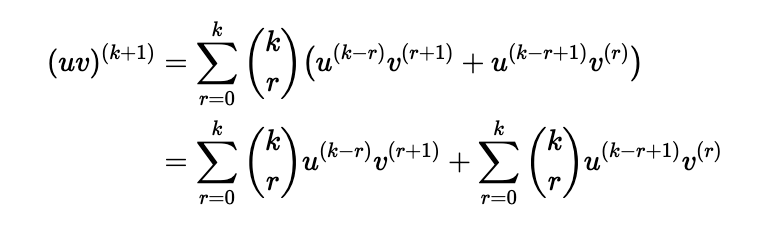
Next, we can rearrange the initial segment of the sum:
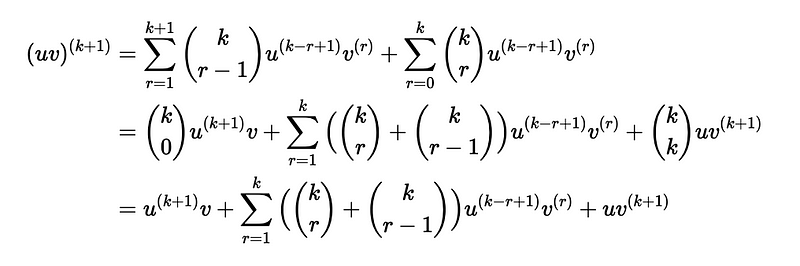
Let’s analyze the sum involving the binomial coefficients present in this equation:
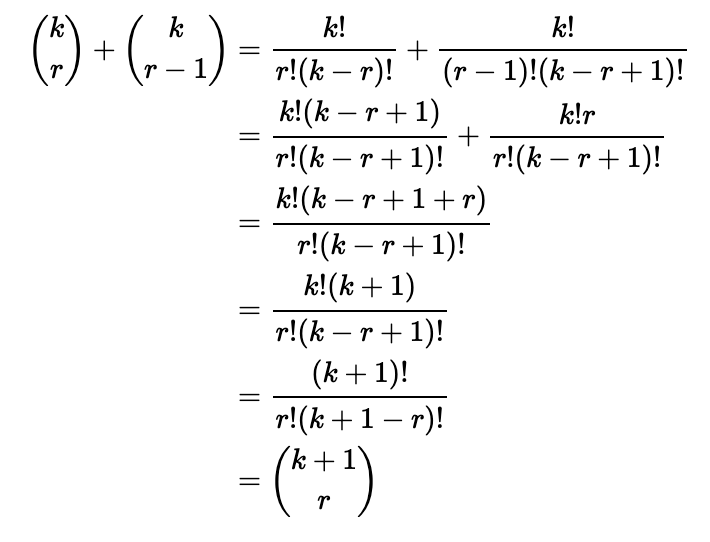
Thus, we simplify to conclude that:
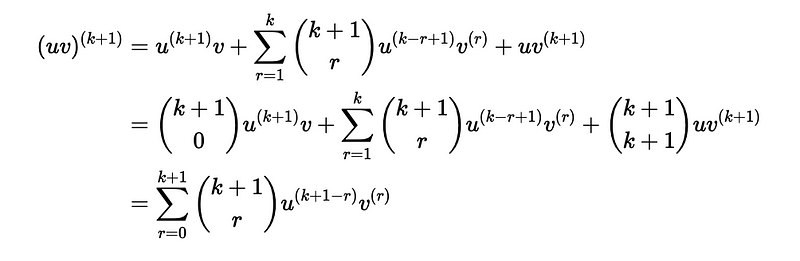
This establishes our result for n=k+1, completing the inductive step and thereby the proof.
Applications of the Derivative Expression
Let’s consider u = sin(x) and v = cos(x). Utilizing this expression, we can derive the fifth derivative of y = sin(x)cos(x):
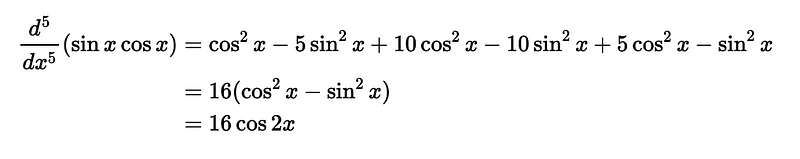
This result is consistent with another approach, which recognizes that sin(x)cos(x) can be expressed as ½sin(2x), allowing us to repeatedly apply the chain rule to achieve the same outcome.
Test Your Understanding
Feel free to try applying the product rule expansion technique to confirm the following:
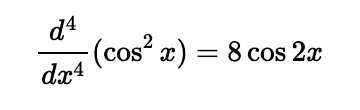
and
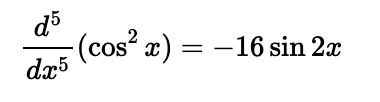
What are your thoughts on this article? I welcome your comments or any other examples of how you can utilize this finding!
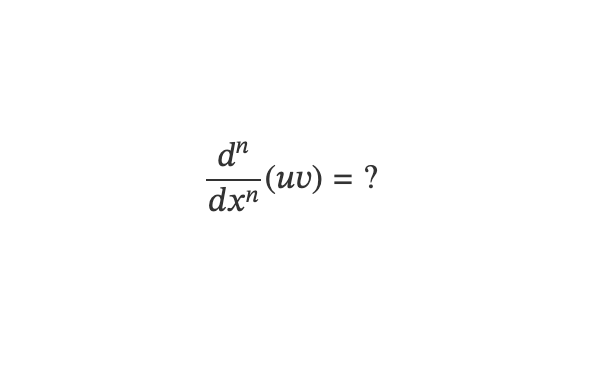
Chapter 2: Videos for Deeper Understanding
To further grasp the concepts discussed, check out the following videos.
The first video, "Extended Product Rule for Derivatives," provides an in-depth explanation of this crucial calculus principle.
The second video, "Leibniz's Rule: Generalization of the Product Rule for Derivatives," expands on the topic, offering insights into its broader applications.