Solving a Challenging Algebra Problem: A Step-by-Step Guide
Written on
Chapter 1 Understanding the Problem
Welcome to the sixth installment in our series on complex algebra problems. Continuing from our last discussion, we remain focused on the secondary school math Olympiad level. In this session, you will face two equations with two variables (x and y):
- Equation 1: x + y = 41
- Equation 2: x * y = 16
The first equation involves the addition of the two unknowns, while the second involves their multiplication. Your goal is to determine the numeric solution to the following intriguing equation:
x √(x) + y √(y) = ??
Do you think you can crack this?
Hint:
Start your journey by applying the binomial square formula.
Spoiler Alert:
I will reveal the solutions beyond this point, so if you want to solve this independently, now's the time to pause.
Once you've made your attempt, feel free to continue reading to see how your method compares to mine.
Applying Logic to the Equations
To make future references easier, let's label the equations as Equation 1 and Equation 2.
After labeling, let’s analyze Equation 2. Since it results in a positive value through multiplication of the two variables, we can conclude that both must be either positive or negative. However, if both were negative, Equation 1 would yield a negative sum, which is not the case here. Thus, we can deduce that:
x > 0 and y > 0
Applying the Binomial Square Formula
Earlier, I hinted at using the binomial square formula to solve this problem. The key here is to recognize that the equation we are attempting to solve includes the square roots of the two unknowns (√(x) and √(y)).
Let's consider applying the binomial square formula to the square of the sum of the square roots of both unknowns. This will help us in simplifying our approach:

Now, we arrive at a numeric result on the right-hand side. We can proceed by taking the square root of both sides:

Let’s label this as Equation 3. The next steps are crucial.
Utilizing the Binomial Cube Formula
This may seem counterintuitive, but the final equation specifically contains the terms ‘x√(x)’ and ‘y√(y)’. We can derive these terms by employing the binomial cube formula.
Let’s clarify this with an example:
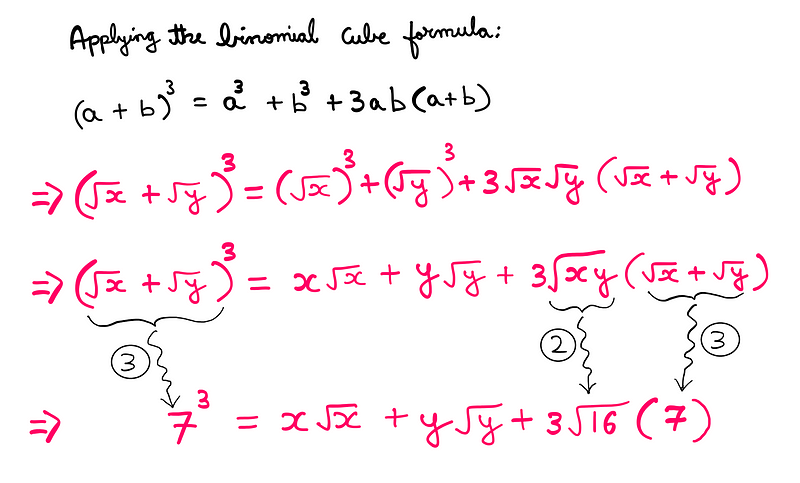
We are nearing the solution; just a few more steps to go.
Solving the Algebra Problem
By substituting the known numeric values from Equations 2 and 3, we can solve the following equation:

The solution to our problem is 259.
If you appreciate my work, consider clapping, following, and subscribing for more content.
For further reading, you might enjoy: "How To Really Solve The Kissing Circles Puzzle?" and "The Resurgence of Big Airships."
If you'd like to support me as an author, please consider contributing on Patreon.