Construction and Challenge

The diagram above illustrates a circle with a radius of 'a,' positioned at the center point C = (0, a). To derive points (x, y), draw a line from the origin O = (0, 0) to any point on the line defined by y = 2a, which we will label as point B. The line intersects the circle at point A. From here, draw a horizontal line through A and a vertical line through B. The intersection of these two lines provides the coordinates (x, y).

Can you determine the area between the Witch of Agnesi curve and its asymptotic line, specifically the space between the red curve and the x-axis?

Part 1: Deriving Parametric Equations

To calculate the desired area as an integral, we must first express the coordinates (x, y) in terms of the angle θ, defined as the angle formed between the positive y-axis and the line OB.

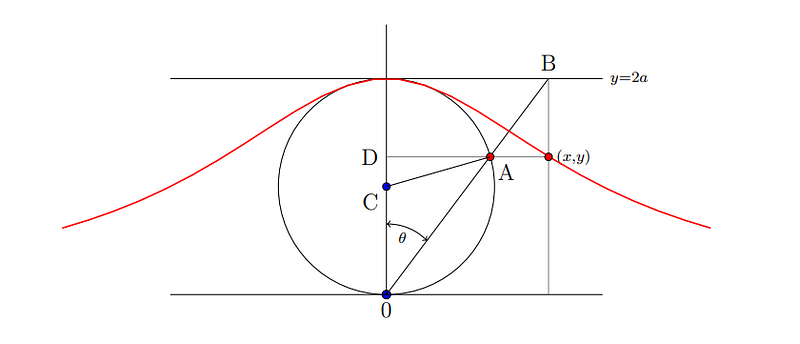
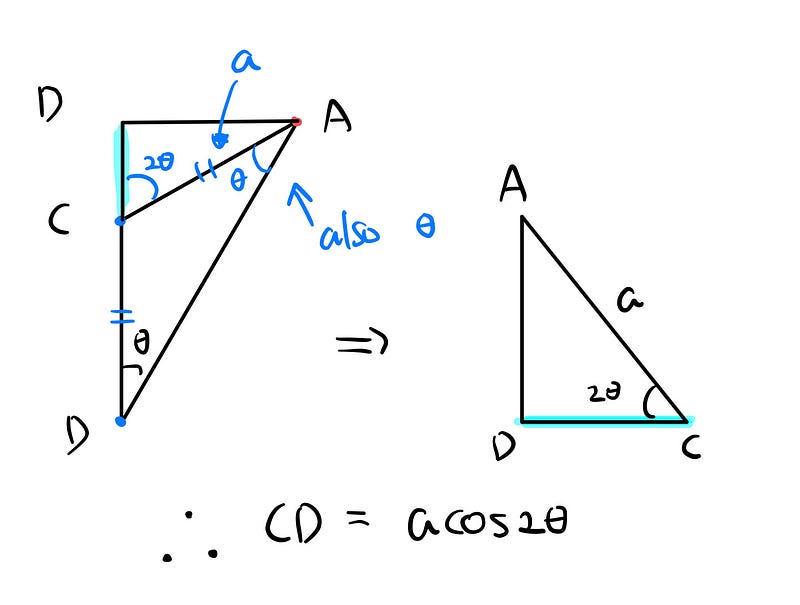
Note that the diameter of the circle is 2a, which means the radius extending from the origin to point C is 'a.' For any point y on the red curve, its length can be expressed as 'a' plus the length of segment CD.

What is the length of CD in terms of 'a' and θ?

Consequently, we can parameterize the y-coordinate accordingly.

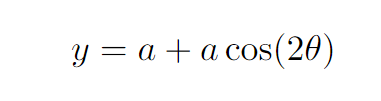
Now, let's examine the x-coordinate.

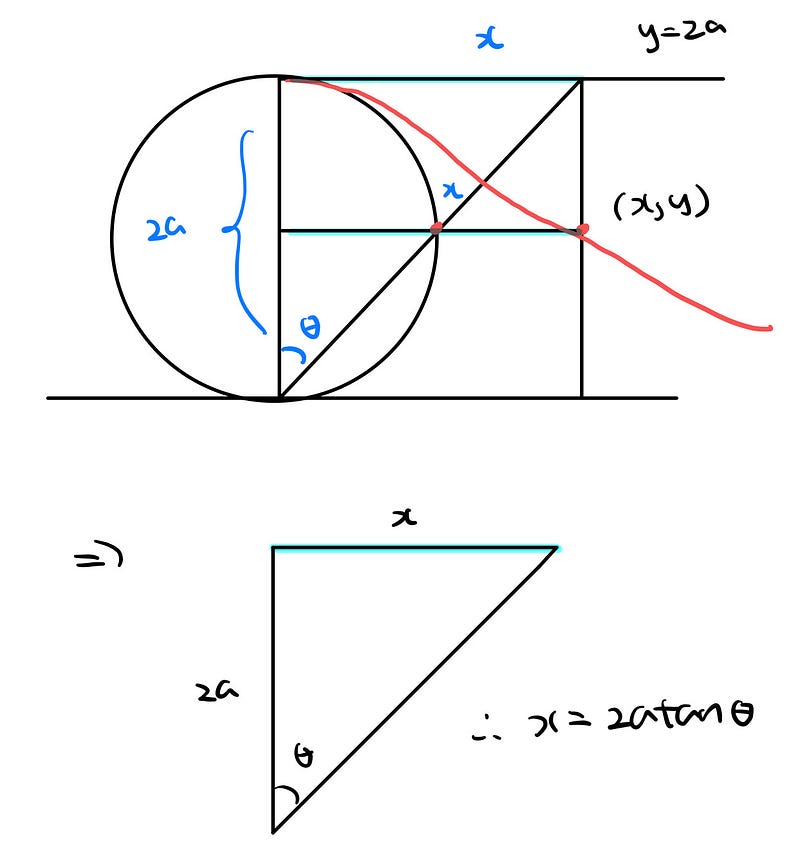
Thus, the x-coordinate can be represented parametrically as follows.

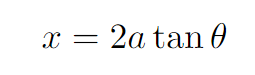
Through further manipulation, we arrive at the following parametrization.

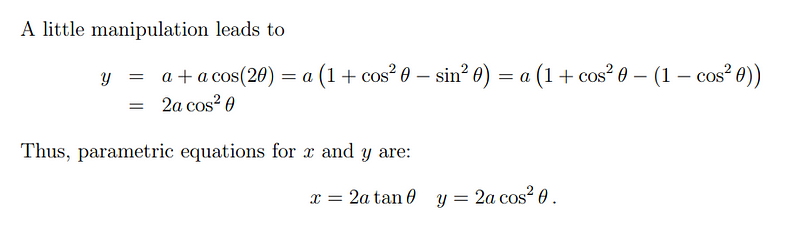
Part 2: Expressing y in Terms of x

To represent the area as an integral, we need to derive a function y in terms of x based on the earlier parametric equations. We'll start by rearranging the expression for x.

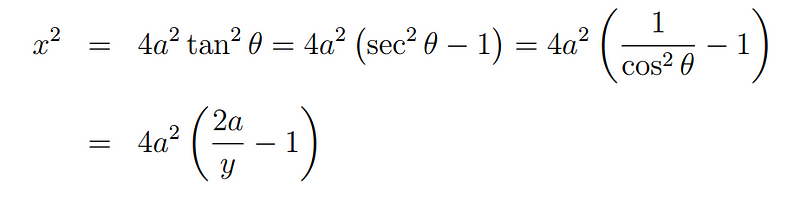
Subsequently, we solve for y to obtain the following result.

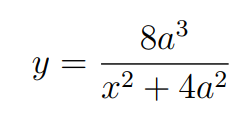
Part 3: Evaluating an Improper Integral

As the area extends infinitely in both directions, we set up the following integral.

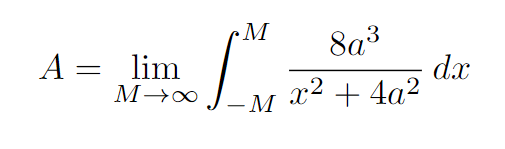
Before proceeding, challenge yourself to compute this integral. For assistance, we start with the following substitution.

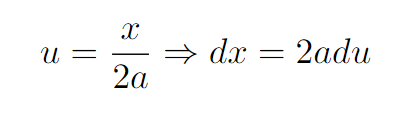
With this substitution, our integral transforms into the following expression.

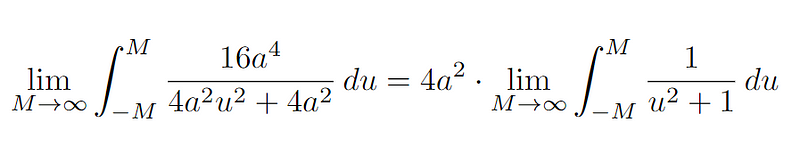
We have now simplified the fraction and factored out 4a².

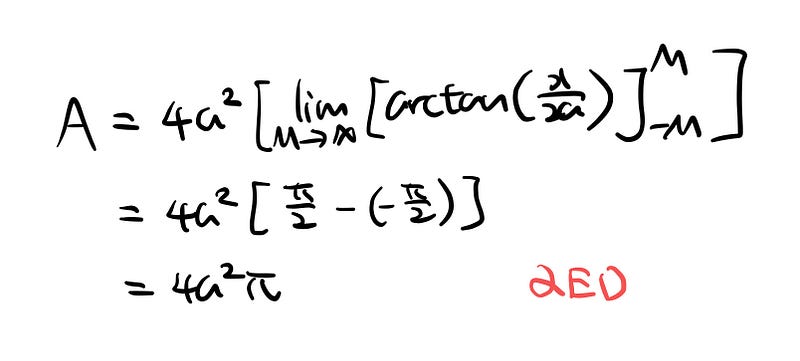
This seems like an excellent point to pause. (Consider examining the graph of arctan(x) to evaluate the limits!) And that's our solution. Isn't that remarkable?

What thoughts did you have during this process? Please share them in the comments below; I'm eager to hear from you! 😊

Math Puzzles

Discover a collection of engaging math puzzles on Medium, covering topics such as Algebra, Geometry, Calculus, and Number Theory. Share this with your friends!

The first video titled "Integration: Area Between a Curve and the x-axis" provides a visual explanation of how to approach finding the area under a curve using integration.

The second video, "Find the area between a curve and the x-axis with integrals," further explores integral calculus techniques essential for calculating areas between curves.

Thank you for reading! If you found this information valuable, please consider showing your support by clapping for this article. Your appreciation motivates my writing.