Chapter 1: Quantum Mechanics Unveiled

Quantum mechanics has fascinated scientists for nearly a century, yet it remains a challenging topic due to its intricate theories and probabilistic nature. As Niels Bohr famously stated, “If you are not completely confused by quantum mechanics, you do not understand it.” This illustrates the complexity inherent in the subject. Despite these difficulties, there are fundamental theories that form the core of contemporary quantum mechanics. One particularly intriguing area of study is quantum computing, which is relevant to my own research. This article will not delve into concepts like superposition or entanglement, but will instead introduce essential notation that will help you grasp these topics more easily when you encounter them.

Section 1.1: Understanding Kets

Let’s begin by examining a standard vector in three-dimensional space…

Basis vectors in a 3D space can be expressed as follows:

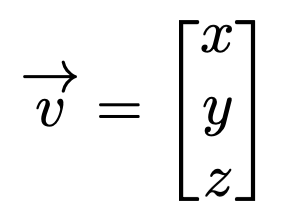
More generally, basis vectors, regardless of their dimensionality, are denoted as:

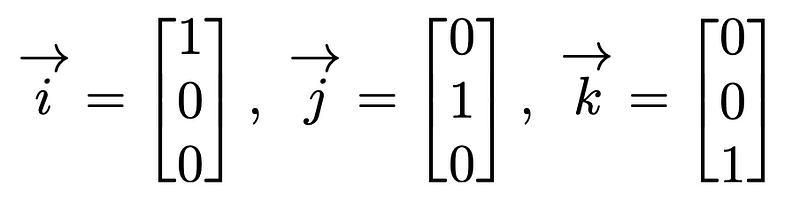
This notation implies that any vector can be represented as a linear combination of basis vectors…

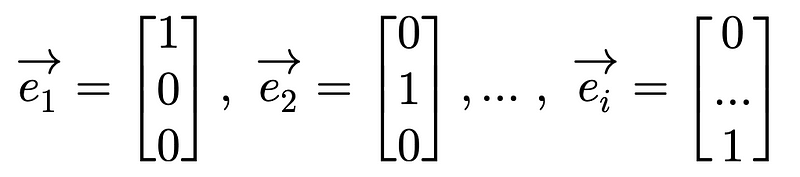
In Dirac notation, we can represent a vector using a ket…

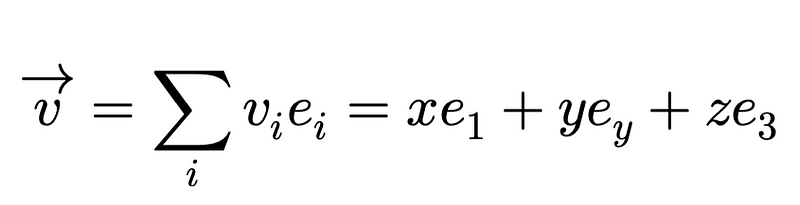
Basis vectors can also be expressed in terms of kets…

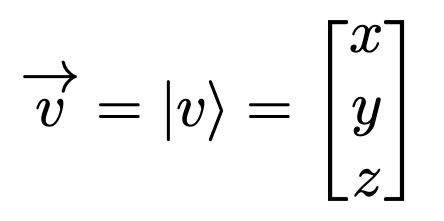
Thus, we can express our original vector as a linear combination of basis vectors using kets…

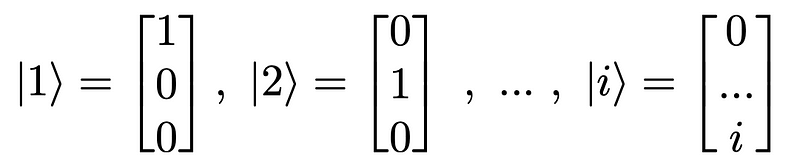
Section 1.2: Exploring Bras

Now, let’s revisit the same vector in three-dimensional space…

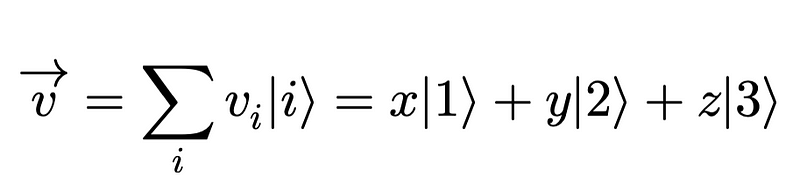
By applying the complex conjugate and transposing, we obtain…

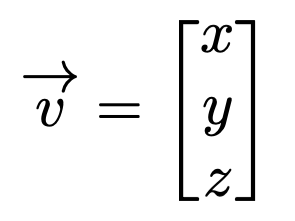
This process turns the column vector into a row vector, and assuming our values are real, the complex conjugate simply yields our original values. This operation is known as the Hermitian conjugate, denoted by a dagger.

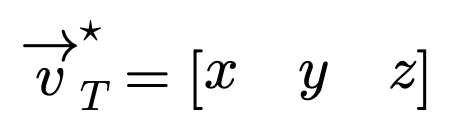
In Dirac notation, this can be represented as a bra vector…

Section 1.3: Bra-Kets Explained

Bras and kets can be combined to signify an inner product, which generalizes the dot product. Considering our original vector in three-dimensional space…

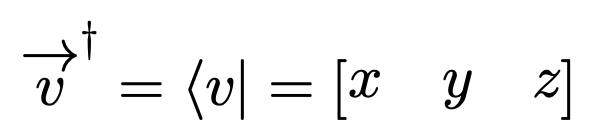
To denote the inner product using Dirac notation between this vector and its Hermitian counterpart, we combine our bra and ket as follows:

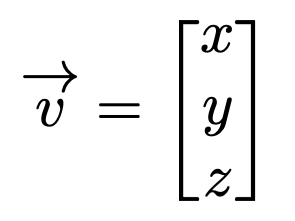
Chapter 2: Conclusion

Quantum mechanics is a field that is as captivating as it is intricate. Its significance is undeniable, particularly with the advent of quantum computing on the horizon. Familiarizing yourself with common notation in this discipline is an essential step towards understanding foundational theories. For those eager to delve deeper into quantum mechanics, I recommend the book No-Nonsense Quantum Mechanics.

This video titled "Introduction to Dirac Notation" provides a foundational overview of the notation used in quantum mechanics.

The video "How to Write Everything in Dirac Notation" offers practical guidance on utilizing Dirac notation for various quantum mechanical contexts.