Mastering Basic Arithmetic with Ruler and Compass Techniques
Written on
Chapter 1: Introduction to Ruler and Compass Arithmetic
Why would someone want to perform basic mathematical operations solely with a ruler and compass? This approach can be traced back to the time of Euclid, a pivotal figure in mathematics. To clarify this notion, let's delve deeper.
In our modern world, children learn the principles of counting and arithmetic through numerical systems. However, during Euclid's era (circa 300 B.C.), the primary mathematical tool was geometry. This meant that the only means of executing basic calculations were the first three postulates from Euclid's Elements, a cornerstone of mathematical literature:
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely into a straight line.
- A circle can be drawn given any straight line segment as the radius, with one endpoint as the center.
- Euclid
Why Perform Math Using Only Ruler and Compass?
To truly appreciate the challenge, we must envision ourselves in Euclid's time, where all mathematical operations had to be completed using only a ruler and a compass (i.e., straight lines and circles). It's worth noting that, in those days, compasses lacked friction to keep their legs apart and would collapse as soon as they were lifted. Additionally, the rulers were unmarked, which means measurements had to be arbitrary. This situation can feel daunting, but let's tackle it step by step.
Addition with Ruler and Compass
We begin by establishing an arbitrary unit of measurement. Let's consider two line segments of lengths 'l' and 'm'.
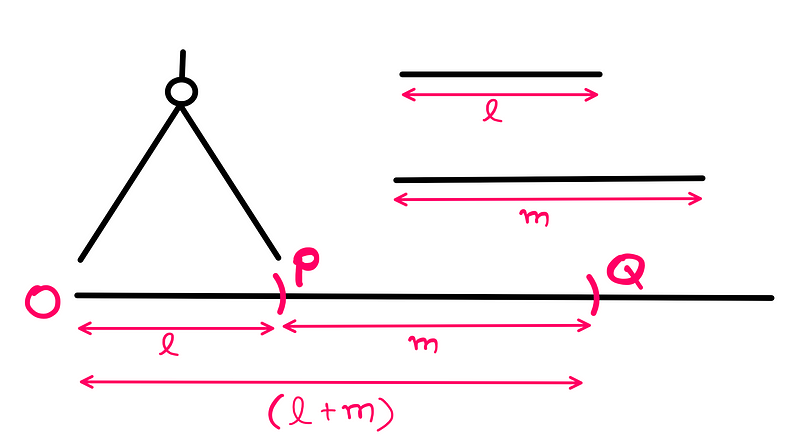
Next, we draw a horizontal line starting at an arbitrary point 'O'. Using a compass, we set 'O' as the center and 'l' as the radius to create an arc that intersects the horizontal line at point 'P'.
With 'P' as the center and 'm' as the radius, we draw another arc to the right, intersecting the line at point 'Q'. The length of segment 'OQ' represents the sum of the two lengths.
Now that we've completed addition, let’s proceed to subtraction.
Subtraction with Ruler and Compass
Using the same setup, we will now calculate the difference between lengths 'm' and 'l' (m-l).
First, we position 'O' as the center again and use 'm' as the radius to cut an arc intersecting the horizontal line at point 'Q'. Then, using 'Q' as the center and 'l' as the radius, we draw an arc to the left, intersecting at point 'P'.
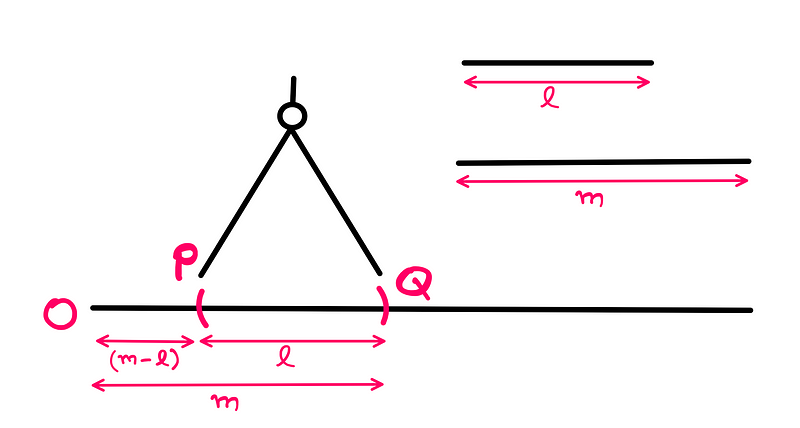
The length of line segment 'OP' now gives us the difference (m-l). With subtraction under our belt, we can now tackle multiplication.
Multiplication with Ruler and Compass
Multiplication introduces a higher level of complexity. The ancient Greeks conceptualized multiplication through areas, making our task a bit more advanced while still adhering to Euclid's postulates.
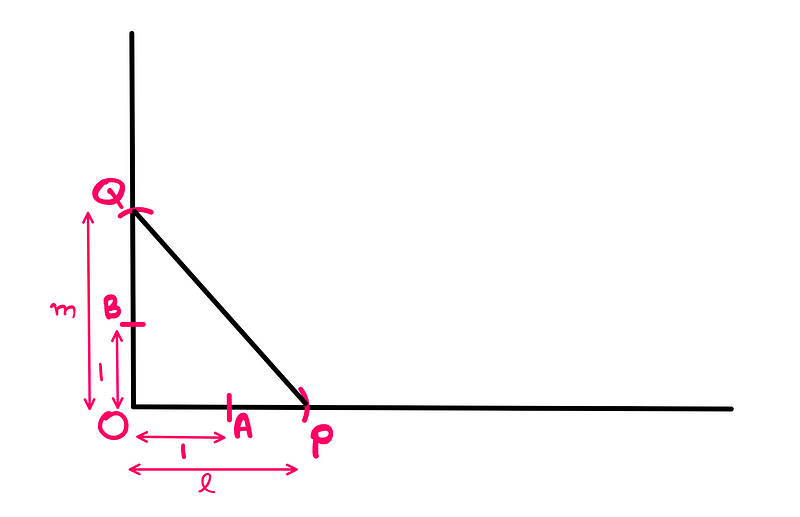
We begin by drawing a vertical line that is perpendicular to our horizontal line at the origin 'O' (creating a makeshift Cartesian system). For guidance on constructing perpendicular lines with a ruler and compass, refer to the appendix.
Now, we mark unit lengths on both lines from 'O'. Let the intersection on the horizontal line be 'A' and on the vertical line be 'B'.
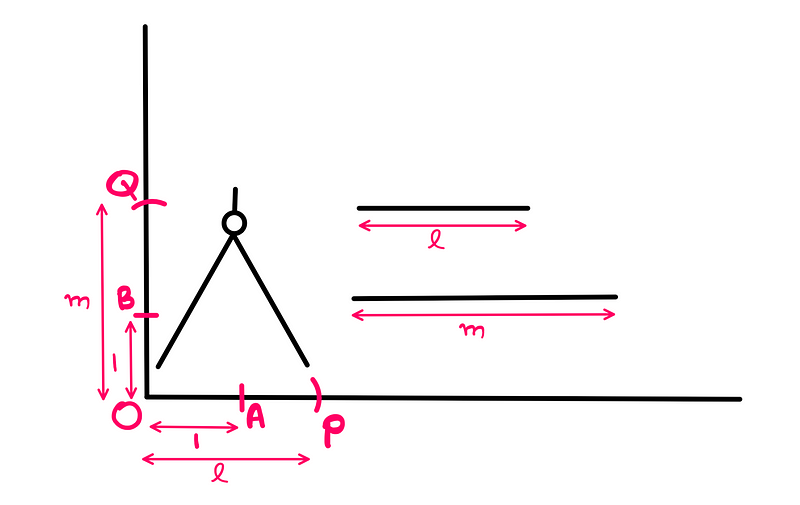
Next, we draw an arc from 'O' with 'l' as the radius on the horizontal line, giving us point 'P'. A similar arc on the vertical line with 'm' as the radius provides point 'Q'.
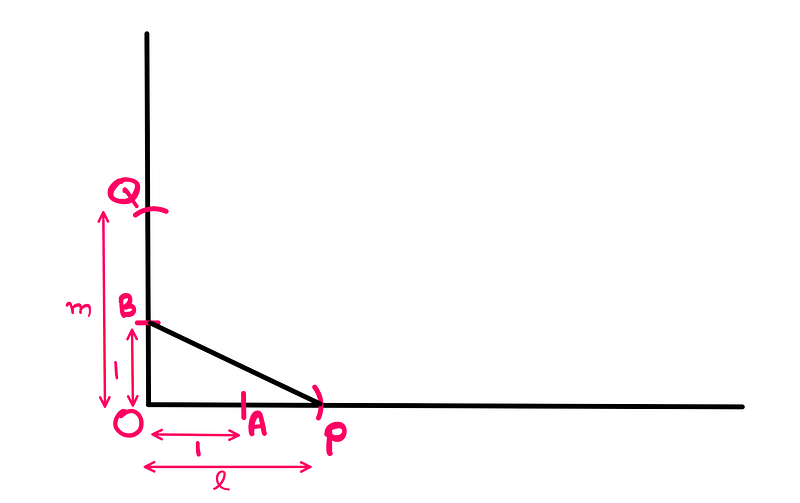
We connect points 'B' and 'P' with a segment 'BP', establishing a relationship between the vertical and horizontal lines. Then, we construct a parallel line from point 'Q' that intersects the horizontal line at point 'C'. The length of segment 'OC' represents the product of 'l' and 'm'.
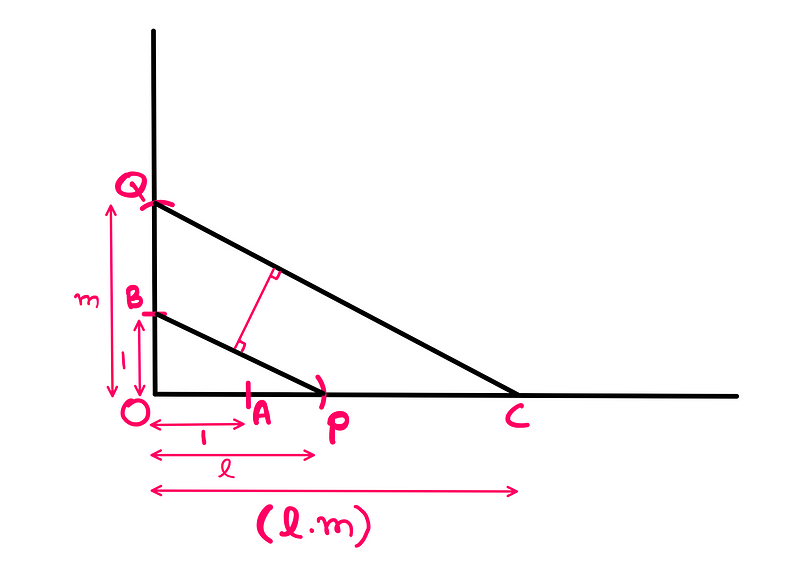
To understand this, note that triangles 'OBP' and 'OQC' are similar, leading to the relationship:
OB/OP = OQ/OC
Substituting known lengths provides:
OC = l*m.
Division with Ruler and Compass
To compute (m/l), we use a setup similar to multiplication:
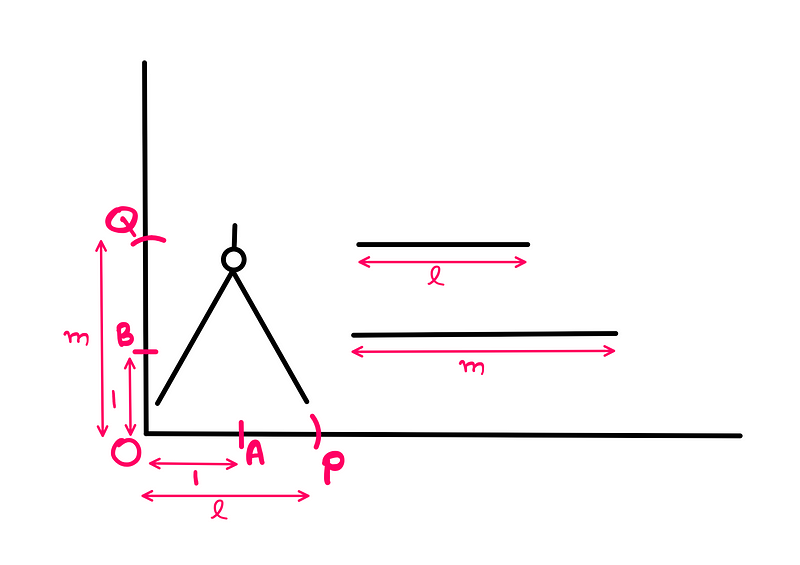
We connect points 'Q' and 'P' to form line segment 'QP', establishing a relationship between the two lines based on lengths 'l' and 'm'.
Constructing a parallel line from point 'P' that intersects the vertical line at point 'C' allows us to determine that the length of segment 'OC' represents (m/l).
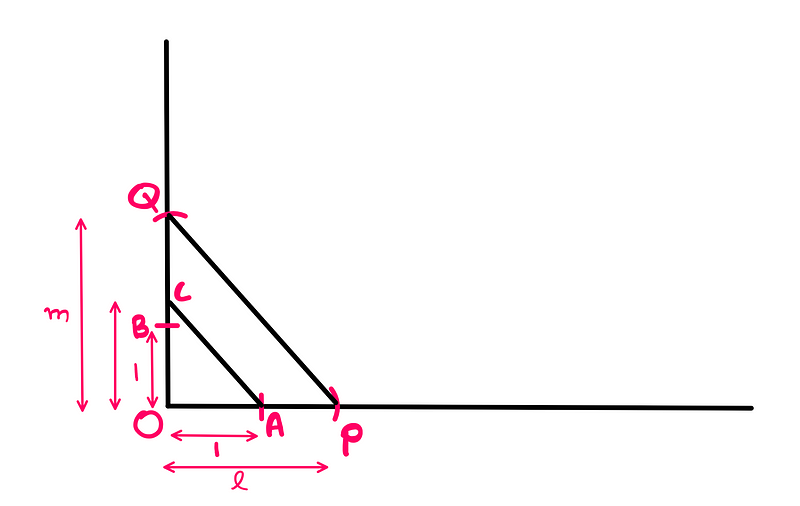
The similarity of triangles 'OCA' and 'OQP' yields the relationship:
OQ/OP = OC/OA
Substituting known lengths results in:
m/l = OC/1, hence:
OC = m/l.
With that, we have successfully executed basic operations of addition, subtraction, multiplication, and division using only a ruler and compass.
Final Thoughts
This exploration is essential as it lays the groundwork for more complex challenges posed by Euclid. Some of the questions he and his followers sought to answer include:
- Can an angle be trisected?
- Is it possible to double a cube?
- Can a circle be squared?
A deeper understanding of these principles is necessary before tackling such inquiries. Expect a follow-up essay addressing these advanced topics soon!
Appendix: Constructing a Perpendicular Line
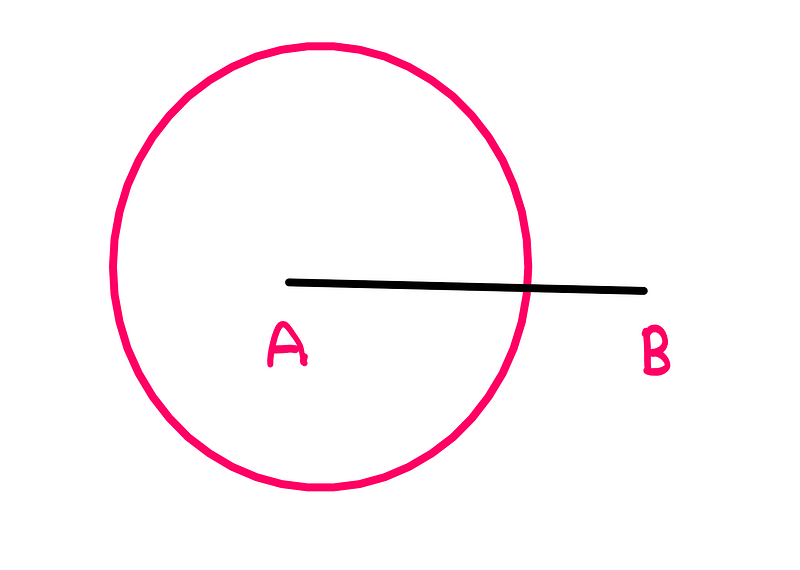
To create a perpendicular line segment 'AB' of arbitrary length, we start by using a compass with point 'A' as the center and length 'AB' as the radius to draw a circle.
Next, we repeat this with point 'B' as the center and radius 'BA', resulting in two intersection points 'C' and 'D'.
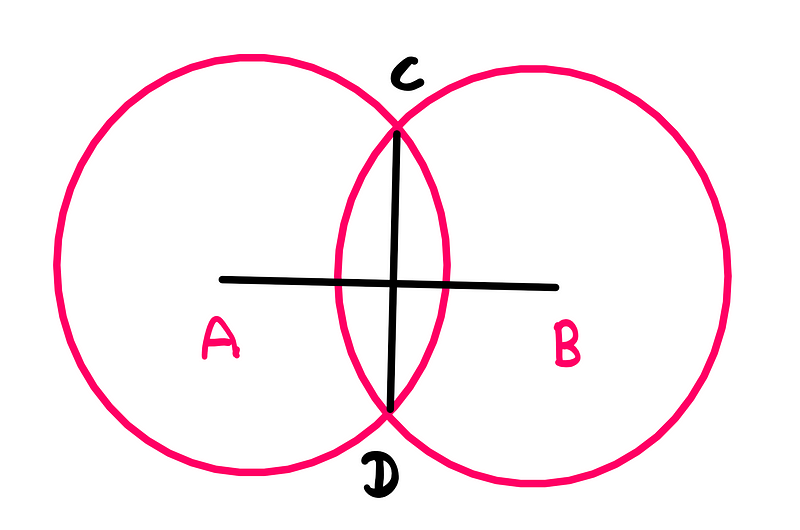
The segment 'CD' formed between these intersections is perpendicular to 'AB' and bisects it.
If you’d like to support my work, consider clapping, following, and subscribing.
Further Reading:
- How To Really Solve 1? = -1?
- How To Actually Subtract Using Addition?
- Why Is 9² Special Among Squares?
For those interested in supporting future content, please consider contributing on Patreon. You can read the original essay [here](#).