Mathematics of Sharing Pizza: A Fun Puzzle with Calculus
Written on
Chapter 1: The Pizza Puzzle
Have you ever wondered how to divide a pizza among three people in a mathematically sound way? The solution is more straightforward than you might imagine! Thanks to the foundational work of Isaac Newton and Gottfried Leibniz, we can apply integral calculus to slice a pizza in an innovative manner—though not in the typical wedge shape.
Imagine a pizza with a radius of 7 inches. Our challenge is to create two parallel cuts through the pizza. The question is: where should these cuts be made? I encourage you to take a moment to think about this using a pen and paper before reading on for the answer!
The first video illustrates how to share three pizzas among six friends, providing insight into fair division.
Solution: Geometric Insights
To comprehend a circle, think of it as being composed of four equal quadrants, each representing one-fourth of the entire area.
This understanding is pivotal to solving our puzzle. The goal is to leverage the symmetry of the circle, which can be divided into four quadrants.

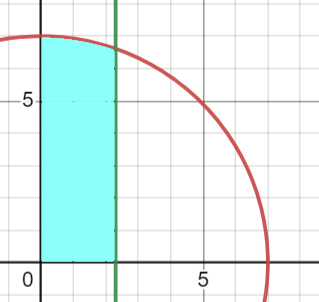
Next, we will make a vertical cut at (x = c), which will divide each quadrant into two sections—one-third and two-thirds. Let's consider the first quadrant; the cut will be made along the line (x = c) and will also affect the second and third quadrants through a symmetrical cut at (x = -c).
As a result, the pizza is divided into three equal portions. Can you see how that works?

If we think of a quarter of the pizza as a single unit, each segment will amount to ( frac{4}{3} ) of a quarter. This calculation checks out: ( left( frac{4}{3} right) left( frac{1}{4} right) = frac{1}{3} )!
Calculating the Value of (c)
Now, we must determine the value of (c) for the vertical cut (x = c) so that the area of the rectangular strip equals one-third of the first quadrant's area.
The equation of the circle is given by:
[ x^2 + y^2 = 49 ]
One-third of the area of the first quadrant can be calculated as:
[ frac{1}{3} left( frac{1}{4} right) pi (7^2) = frac{49pi}{12} ]
Next, we set up a definite integral with limits from (x = 0) to (x = c) to match the area calculated above.
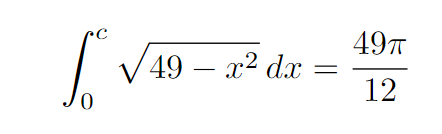
Are you familiar with solving integrals? One approach is to use the substitution (x = 7sin(theta)). If done correctly, you should arrive at a complex expression.
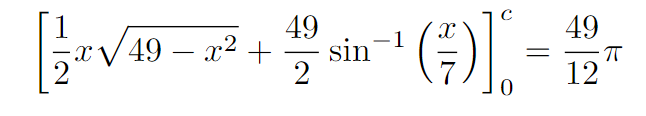
However, solving for (c) algebraically can be quite intricate.
Utilizing Graphing Tools
To find an approximate value for (c), we can use Desmos to plot the function.
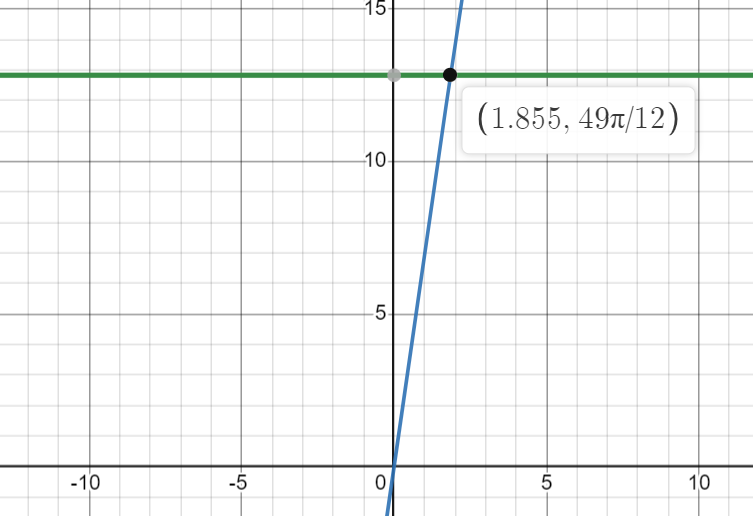
From the graph, we discover that (c) is approximately 1.85 inches from the y-axis. Now you know how to mathematically share a pizza with friends! (Will you treat me to a slice?)

What do you think of this puzzle? I'd love to hear your thoughts in the comments!
Chapter 2: Cake Division
The second video explores the concept of equally sharing a cake among three people, providing further insights into fair division strategies.
Thank you for engaging with this mathematical exploration. If you found this article helpful, please consider giving it a clap!