Chapter 1: The Illusion of Light-Speed Travel

What would it truly be like to circle the Earth at the speed of light? Surprisingly, it wouldn't resemble any of our common visuals.

An airplane zipping through the cosmos at light speed?

I recently came across an intriguing YouTube video that offers a striking representation of light's astonishing speed (and, in contrast, highlights how much slower sound travels).

However, I must clarify: the depiction shown in the video doesn't accurately portray what traveling around Earth at light speed would entail.

So, what would it actually look like? Well, the answer is simple—it wouldn't look like anything at all.

According to the principles of Special Relativity, as you accelerate relative to an object—such as Earth—the object's length appears to contract.

The equation governing this length contraction is:

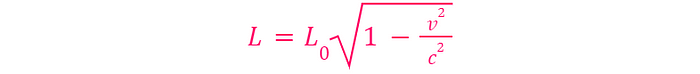
Where L₀ represents the rest length of an object (the length observed when both you and the object are stationary). Here, v is your speed in relation to the object, and c signifies the speed of light.

For instance, if you travel at 80% of light speed past a house that measures 10 meters, you would perceive the house as being only 6 meters long.

Now, if you were to reach 100% of light speed? In this case, v equals c, leading to v²/c² equating to 1. Therefore, 1 - 1 results in 0, making the right side of the length contraction equation 0. This means L = 0.

This conclusion holds true irrespective of L₀. In simpler terms, anything observable would have a length of 0. There would be no path to traverse; nothing would possess any length at all. (Keep in mind that this only applies to the dimension parallel to your travel direction—objects still retain width.)

So, if everything appears to have zero length, what does that imply for our perception?

Once more, the answer is that it wouldn't appear as anything—because there wouldn't be time to observe anything at all. Time itself would also contract (or dilate) to 0, as indicated by the following formula:

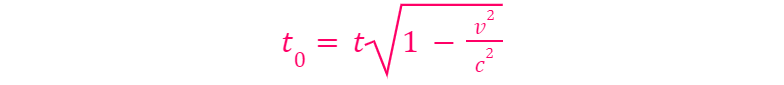
This formula illustrates that regardless of how much time elapses for those on Earth (t), the time experienced by us traveling at light speed (t') would be 0. Thus, there would literally be no time available to witness or experience anything, since experiencing requires time.

Moreover, this discussion overlooks the significant issue of colliding with air molecules while traveling at light speed—a catastrophic impact that would necessitate an extraordinarily advanced aircraft for survival.

On the other hand, achieving light speed would also lead to infinite mass, suggesting that, theoretically, anything could occur.

Thank you for taking the time to read this! If you wish to support Street Science, feel free to consider contributing through Patreon.

Chapter 2: The Paradoxes of Light Speed

No youtube to insert. Don't generate youtube directive.