Chapter 1: The Nature of Spacetime

In the realm of general relativity, we treat space and time as intertwined components of a unified entity known as spacetime. This spacetime is characterized as a smooth and coordinate-friendly structure, referred to as a manifold. The metric ( g ) allows us to precisely define distances and the lengths of vectors within this manifold. We can think of our metric as a matrix that varies at different points in the manifold, and solving for this metric involves addressing the Einstein field equations.

The central inquiry revolves around which types of metrics are permissible within the framework of general relativity. It's not feasible to arbitrarily select any metric and assume it's valid. Thus, what metrics can exist in nature? Are there governing dynamics that dictate how they evolve through space and time? Is there an equation to determine how a metric changes?

These inquiries are valid and important. It turns out that the metrics that can exist in a physical sense are solutions to the equations known as the Einstein field equations. Below, I've included these equations.

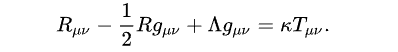
The equation is quite complex. On the right, the symbol ( T ) denotes the energy-momentum tensor, which encapsulates the energy present in our spacetime, such as that of a neutron star. This tensor influences the curvature of spacetime based on the type of matter present.

On the left side of the equation, we find various symbols that describe the fundamental properties of spacetime. The symbols associated with ( R ) reveal how "curved" spacetime is. The first term, known as Ricci curvature, outlines how spacetime deviates from a flat geometry. The second term indicates how our concept of volume differs from a flat space perspective, referred to as the Ricci Scalar. Finally, the cosmological constant and the metric itself complete the equation.

In this discussion, I aim to outline how this equation can be derived.

Section 1.1: The Einstein-Hilbert Action

We will treat the metric as a dynamic variable, akin to how we handle the position of a particle in classical mechanics. As previously discussed, we first create an action by integrating a Lagrangian over a set time interval. To derive the path of a classical particle, we seek the trajectory that minimizes the action.

In general relativity, we similarly construct an action incorporating the metric. This involves devising a function of the metric that is plausible and then verifying whether the resulting equations of motion align with classical predictions. This process blends creativity and mathematical rigor.

After constructing an action based on the metric, we attempt to minimize it to ascertain the precise form of the metric. The resulting metric then becomes a solution to the Einstein field equations. While minimizing the action poses a technical challenge, we only need to perform the calculation once.

Subsection 1.1.1: Formulating the Einstein-Hilbert Action

The action we will derive from the metric is termed the Einstein-Hilbert action. Given that our primary focus is the metric, we have limited options for variation. The only variable we can manipulate is the metric ( g ).

The "volume" of an object in spacetime is fundamentally dependent on how distances are defined. A natural approach to define volume within spacetime is to utilize the square root of the metric's determinant. This leads us to conclude that our action should commence with something resembling:

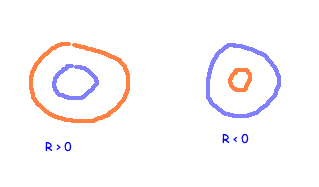
Next, we need a scalar function to incorporate. The Ricci Scalar, a real number that takes a value at each point in the manifold, is the only logical choice. When the Ricci Scalar is positive, it indicates that the volume of a small sphere around that point is less than if it were measured using a flat, Euclidean metric. Conversely, a negative Ricci Scalar suggests a larger volume.

Thus, the most intuitive way to formulate the action is by placing the Ricci Scalar before the volume form, as expressed in the equation below:

Furthermore, the Ricci curvature tensor also measures how the curvature of a space contrasts with flat space.

Section 1.2: Extremizing the Einstein-Hilbert Action

To derive the Einstein field equations, we must identify the metric that minimizes the action. We achieve this by introducing a slight perturbation to the metric and observing the resulting change in the action ( S ). We anticipate that ( S ) will change marginally, and we will express this variation mathematically.

In mathematics, a slight change is referred to as a "perturbation." Thus, we represent our perturbed metric by adding a small term, denoted by the Greek letter delta.

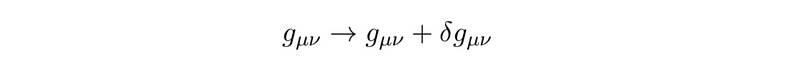
When we perform this variation, we must express the Ricci Scalar in terms of the Ricci tensor contracted with the metric. Using the product rule for small variations, we can expand the expression. It is crucial to remember to apply this variation to the volume form and consider how it alters with the metric.

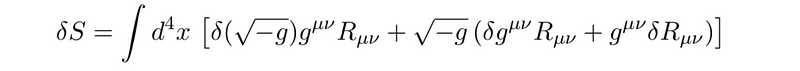
To derive the equations of motion, we rearrange the terms within the integral to isolate a common expression that can be set to zero. This simplification process can be complex, but the outcome reveals that:

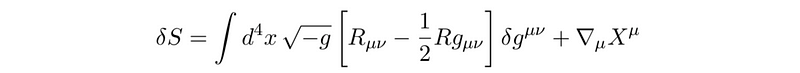
The tensor denoted by ( X ) signifies a boundary condition. By imposing the stationarity requirement for any changes in the metric, we derive the vacuum Einstein equations. This term refers to the condition where we assume the absence of mass or energy.

The equation provided is precisely the Einstein field equations in a scenario devoid of energy or mass, where we have assumed that most constants equal one.

Chapter 2: Filling in the Fundamental Constants

Utilizing dimensional analysis, we can determine the constants required in our action. The action ( S ) possesses dimensions of ( ML^2/T ), while the metric remains dimensionless, and ( R ) carries units of ( 1/L^2 ). To ensure our action is dimensionally consistent, we need to introduce constants to balance the dimensions, leading us to the full action represented as:

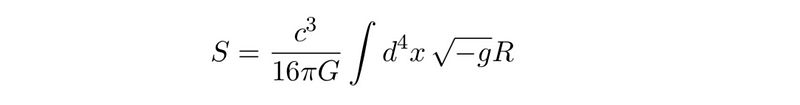
With these constants integrated, we can fully recover Einstein’s field equations. In my next post, I will explore some straightforward solutions to these equations and their fascinating properties.

In the first video, titled "General Relativity Basics - Einstein Field Equation Derivation," the foundational concepts of Einstein's field equations are introduced, providing a clear understanding of their derivation.

The second video, "Einstein Field Equations - for beginners!" offers an accessible overview of Einstein's field equations, perfect for those new to the topic.