Chapter 1: Introduction to the Galton Board

The Galton board, created in 1876 by the brilliant Sir Francis Galton, serves as a sophisticated illustration of how a normal distribution emerges from numerous random events. This invention provided Galton with crucial insights into the distribution of human traits while he was researching heredity. It also significantly contributed to the formation of statistical theory, concepts that still hold great importance today.

The distribution occurs as beads traverse a grid of pegs, where each bead randomly shifts left or right upon hitting a peg. This setup allows beads to follow various paths before settling into one of the bins below.

When examining the center of the pattern, one can observe numerous routes leading to the middle bins. Conversely, as you move outward, the available pathways decrease significantly.

With 12 rows of pegs, there are 463 distinct paths a bead can take to reach the central bins, compared to only a single path to the extreme outer edges.

Chapter 2: The Role of Pascal’s Triangle

However, the significance of these figures extends beyond mere counting. There exists a recognizable pattern, and Pascal’s Triangle is one of the most renowned patterns in mathematics.

Pascal's Triangle has been a subject of study for centuries. To construct it, begin with a single "1" at the top. From there, continue placing "1s" on both sides while filling in the middle with the sum of the two numbers directly above. This method reveals how the pattern evolves.

In fact, the numbers generated from this triangle directly correlate to the various paths a bead can take on the Galton board. The bead's journey is a binomial process, where the numbers of Pascal's Triangle align with the coefficients found in a binomial expansion.

The concept of binomial distribution arises from conducting a series of Bernoulli trials, which involve flipping a coin—resulting in heads or tails, yes or no, zero or one. When you combine several of these trials, you arrive at a binomial distribution. This distribution is intricately linked to binomial expansion.

In this video titled "Galton Board and Pascal's Triangle," you'll gain insights into how these mathematical concepts intersect.

Each term in a binomial expansion has a coefficient indicating how often that term appears when the expression is multiplied out. These coefficients are referred to as binomial coefficients, which stem from the presence of two quantities (x and y) in the expansion process.

These coefficients are not merely theoretical; they have practical applications, particularly in combinatorics. For example, if you have four individuals and wish to form a team of two, the binomial coefficient reveals there are six distinct ways to make this selection. This can be easily identified from the corresponding row of Pascal's Triangle.

By examining the fourth row and second element, we discover six different combinations to choose two people from a group of four.

Chapter 3: Combinatorics and Probability

Understanding these combinatorial principles is vital for calculating probabilities. For instance, if you flip a coin 11 times and want to determine the likelihood of obtaining two heads, you need to consider all the various sequences of flips.

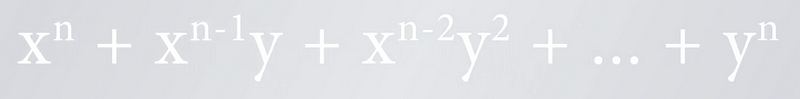
To find out how many ways you can achieve two heads out of 11 flips, you can directly refer to the binomial coefficient from Pascal's Triangle. There are 55 unique combinations for selecting the positions of these two heads among the 11 flips, which leads to a probability of approximately 3%.

But how do we determine the total number of possible sequences? The answer lies within the structure of Pascal’s Triangle, which consists of 12 rows. Each row's sum provides the total number of possible outcomes for a certain number of flips. For example, when flipping a coin three times, the total combinations can be calculated as 1 + 3 + 3 + 1, yielding eight possibilities.

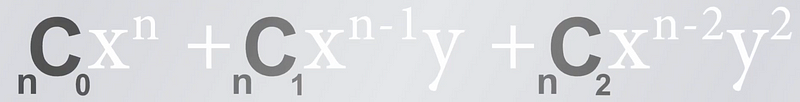
As we progress down the triangle, a clear pattern emerges—these sums correspond to the powers of two. If you flip a coin four times, you will find 16 possible outcomes, and for 11 flips, there are 2048 combinations of heads and tails.

This phenomenon mirrors what occurs in the Galton board with its 12 rows of pegs, paralleling the act of flipping a coin between two options. We can question the probability of where each bead will land.

When considering a Galton board with 11 rows, every time a bead strikes a peg, it presents a binary choice analogous to a coin flip. The total number of pathways through the board is 2^11, equating to 2048. To find the probability of a bead landing in a specific bin, we divide the number of paths leading to that bin by the total pathways available.

For example, if there are 462 pathways leading to one of the middle bins, we divide 462 by 2048 to ascertain the probability that a bead will settle in that bin, which is roughly one-quarter of the time. When combining both central bins, this probability increases to nearly 50%.

There exists a mathematical formula for calculating these binomial coefficients, but with Pascal's Triangle, you can easily derive them. This elegant system allows you to visualize how many beads are expected to land in each bin, creating the beautiful normal distribution observed.

The Galton board can be seen as a dynamic representation of Pascal’s Triangle. If you're interested in acquiring a Galton board for educational purposes at your school, museum, or even your home, it is available for purchase on Amazon.

Note: As an Amazon Associate, I earn from qualifying purchases.

In the video titled "Galton Board with Pascal's Triangle," you'll discover more about the fascinating relationship between these two mathematical concepts.