Chapter 1: Overview of the MIT 2024 Integration Bee

In January 2024, eight exceptional students were chosen to participate in the MIT Integration Bee semifinals, having proven their mettle among a pool of talented candidates. While many aspire to qualify and win, ultimately only one can emerge victorious. This article delves into one of the intriguing problems featured in the semifinals. Notably, the competition is not solely based on difficulty; it emphasizes speed. However, this does not imply that the problems are simple. The challenge presented had a mere four-minute time limit. Do you think you can outpace a top integrator? Before checking the solution, take a moment to try solving the problem on your own.

The denominator resembles a geometric series, particularly influenced by the negative exponent in the exponential function. Therefore, it’s prudent to express it as follows:

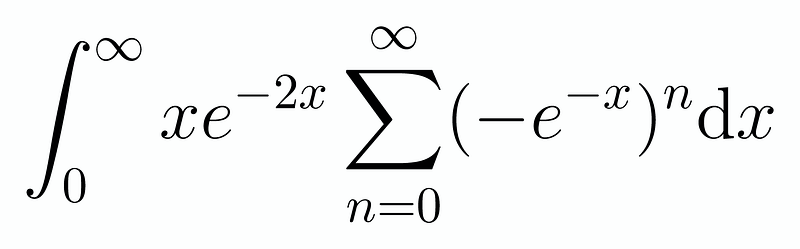
Next, we can reformulate it as:

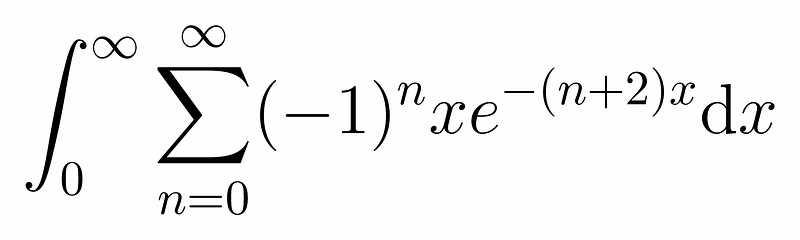
By interchanging the integral and the summation, we arrive at a more manageable integral:

This integral is relatively straightforward. We can either apply integration by parts once or utilize the substitution ( u = (n+2)x ), quickly leading us to the gamma function's form. Regardless of the approach, we are left with just a summation. This summation is:

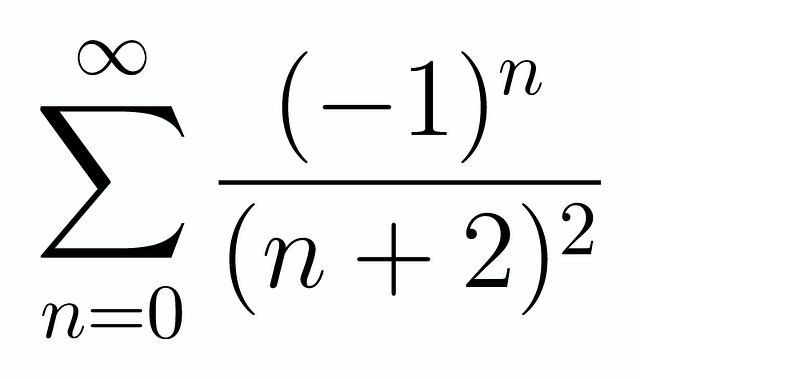
This should instantly remind us of the Basel problem, where the sum of the squares of the reciprocals equals ( frac{pi^2}{6} ). By rearranging, we recognize that this sum is equivalent to:

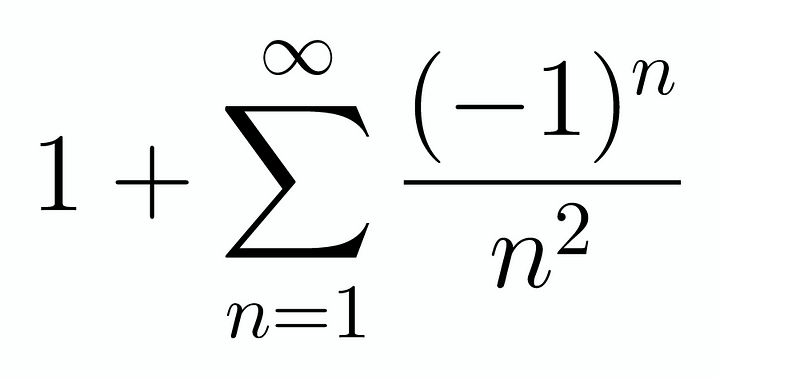
Since this series converges absolutely, we can separate it into odd and even terms without altering the overall sum. The challenge is determining these values. If we temporarily ignore the alternating nature of the series, the total sum would indeed be ( frac{pi^2}{6} ). Focusing solely on the even terms yields:

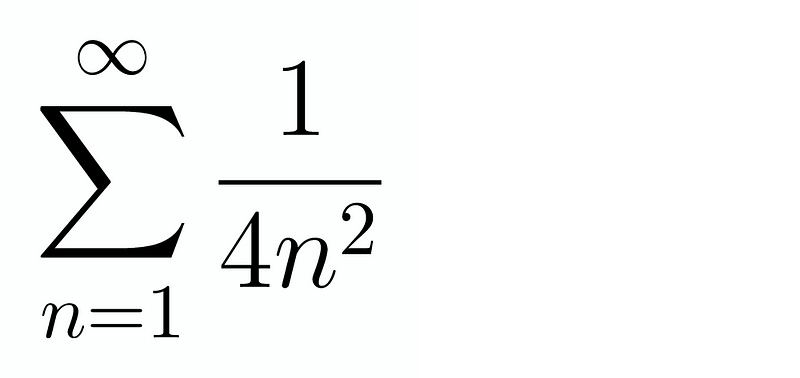
This represents a quarter of the total sum of squares of the reciprocals, thus it must equal ( frac{pi^2}{24} ). Given that the sums of the odd and even terms must equate to the total, the sum of the odd terms must be ( frac{pi^2}{8} ). Returning to our expressions, let’s denote the sums of odd and even terms as ( B_{text{odd}} ) and ( B_{text{even}} ). Therefore, our sum can be expressed as:

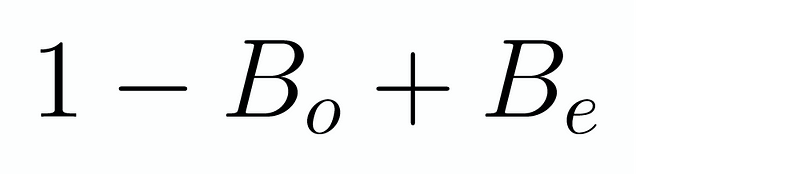
In conclusion, we can consolidate our findings into:

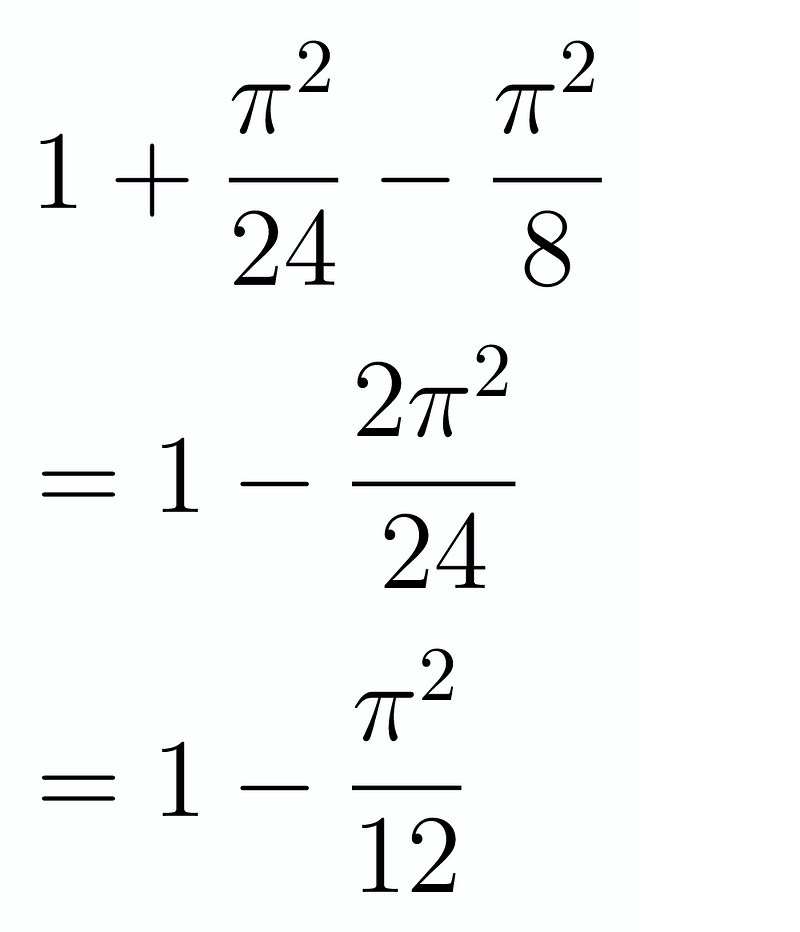
Our final result is:

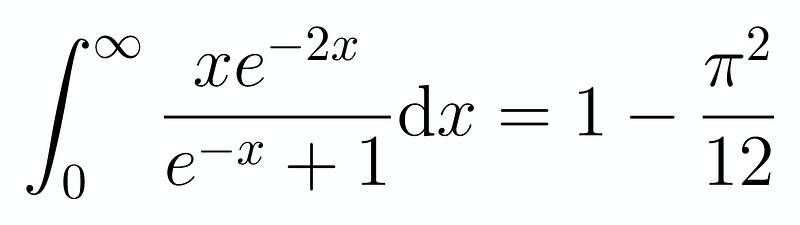
Were you able to solve it? Moreover, did you complete it in under four minutes?

If you found this article enjoyable, consider supporting me! Your contributions are greatly appreciated! For further insights into the MIT Integration Bee, feel free to explore more here.

Chapter 2: Video Insights from the MIT Integration Bee

Explore the semifinals' solutions with this insightful video that breaks down various problems faced by the participants.

Delve into Problem 1 of the MIT 2024 Integration Bee semifinals with this focused video, offering detailed explanations and solutions.